题目内容
如图所示，质量M、带有半球型光滑凹槽的装置放在光滑水平地面上，槽内有一质量为m的小铁球，现用一水平向右的推力F推动凹槽，小铁球与凹槽相对静止时，凹槽球心和小铁球的连线与竖直方向成α角，则下列说法正确的是（ ）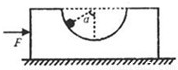
A．推力F=Mgtanα
B．系统的加速度为a=gtanα
C．凹槽对小铁球的支持力为
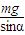
D．小铁球受到的合外力方向水平向左
【答案】分析：小球的加速度方向与凹槽的加速度方向相同，都是水平向右，分别对小球和凹槽进行受力分析，运用牛顿第二定律即可分析求解．
解答：解：B、对小球进行受力分析得：
mgtanα=ma
解得：a=gtanα，故B正确，
A、对整体进行受力分析，根据牛顿第二定律得：
F=（M+m）a=（M+m）gtanα，故A错误；
C、凹槽对小铁球的支持力N=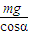
，故C错误，
D、小球的加速度方向水向右，所以合外力方向水平向右，故D错误．
故选B
点评：本题主要考查了同学们受力分析的能力，注意小球与凹槽的加速度相同，难度不大，属于基础题．
解答：解：B、对小球进行受力分析得：
mgtanα=ma
解得：a=gtanα，故B正确，
A、对整体进行受力分析，根据牛顿第二定律得：
F=（M+m）a=（M+m）gtanα，故A错误；
C、凹槽对小铁球的支持力N=
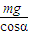，故C错误，D、小球的加速度方向水向右，所以合外力方向水平向右，故D错误．
故选B
点评：本题主要考查了同学们受力分析的能力，注意小球与凹槽的加速度相同，难度不大，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
