Question

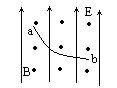
如下图所示，在空间有水平方向的匀强磁场和竖直方向的匀强电场，场强为E，磁感应强度为B，在场区某点由静止释放一个带电液滴a，它运动到最低点处，恰为一个原来静止的液滴b相碰，碰后合为一体沿水平方向做直线运动．已知液滴a的质量是b的2倍，液滴a所带电量是b的4倍，求两液滴初始位置之间的高度差h．(设a、b间的静电力不计)

Answer 1

答案：
解析：

由于b静止在场中，则b一定带正电，设b的质量、电量各为m和q，b受力平衡，有　　　　　　　　　　　　    　　　　    mg＝Eq　　　　　　① 　　开始a仅受重力2mg、电场力4Eq，向下运动而后又在洛仑兹力作用下向右偏转，由左手定则知a只能带负电，设a与b碰时速度为v0，碰后共同速度为v，则由动量守恒得： 　　　　   2mv0＝3mv　　　　　② 碰后的电量为 　　　　  Q＝－4q＋q＝－3q　　　③ 碰后又沿直线运动，故有 　　　　  3mg＋3Eq＝3Bqv　　　　④ a由初始位置下落到最低点的过程中，洛仑兹力不做功，则由动能定理得 　　　　 4Eqh＋2mgh＝　　　　⑤ 解以上5式联立得：   h＝

提示：

思路分析　　由于b静止，则知b带正电，且mg＝Eq，而a开始时向下运动且向右偏转，故由左手定则知a必带负电．a和b碰后沿直线运动，则受力必定平衡，则有2mv0＝3mv，3mg＋3Eq＝3Bqv．再对a列出动能定理列式即可求出结果．