题目内容
 如图所示,M为固定在水平桌面上的有缺口的方形木块,abcd为
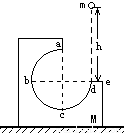
如图所示,M为固定在水平桌面上的有缺口的方形木块,abcd为 圆周的光滑轨道,a为轨道的最高点,de面水平且有一定长度.今将质量为m的小球在d点的正上方高为h处由静止释放,让其自由下落到d处切入轨道内运动,不计空气阻力,则( )
圆周的光滑轨道,a为轨道的最高点,de面水平且有一定长度.今将质量为m的小球在d点的正上方高为h处由静止释放,让其自由下落到d处切入轨道内运动,不计空气阻力,则( )A.在h一定的条件下,释放后小球的运动情况与小球的质量有关
B.只要改变h的大小,就能使小球通过a点后,既可能落回轨道内,又可能落到de面上
C.无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内
D.无论怎样调节h的大小,都不可能使小球飞到de面之外(即e的右侧)
【答案】分析:释放后小球的运动情况与小球的质量无关.根据机械能守恒定律和向心力知识求出小球恰好通过a点时平抛运动的水平距离,判断小球能否落回轨道内.
解答:解:
A、释放后小球的加速度与小球的质量无关,则其运动情况也与小球的质量无关.故A错误.
B、C、D设小球恰好通过a点时速度为v,圆周的光滑轨道半径为R,则有mg=m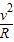 ,v=
,v=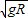
小球离开a点做平抛运动,则平抛运动最小的水平距离为s=vt=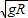
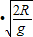 =
=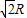 >R,可见,无论h多大,s>R,无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内.故BD均错误,C正确.
>R,可见,无论h多大,s>R,无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内.故BD均错误,C正确.
故选C
点评:本题中小球恰好到达a点时轨道对小球的弹力为零,由重力提供向心力,临界速度为v临=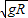 .
.
解答:解:
A、释放后小球的加速度与小球的质量无关,则其运动情况也与小球的质量无关.故A错误.
B、C、D设小球恰好通过a点时速度为v,圆周的光滑轨道半径为R,则有mg=m
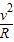 ,v=
,v=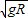
小球离开a点做平抛运动,则平抛运动最小的水平距离为s=vt=
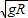
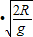 =
=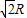 >R,可见,无论h多大,s>R,无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内.故BD均错误,C正确.
>R,可见,无论h多大,s>R,无论怎样改变h的大小,都不可能使小球通过a点后落回轨道内.故BD均错误,C正确.故选C
点评:本题中小球恰好到达a点时轨道对小球的弹力为零,由重力提供向心力,临界速度为v临=
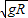 .
. 
练习册系列答案
相关题目
 如图所示,M为固定在桌面上的木块,M上有一个
如图所示,M为固定在桌面上的木块,M上有一个| 3 |
| 4 |
| A、在h为一定值的情况下,释放后,小球的运动情况与其质量的大小无关 |
| B、只要改变h的大小,就能使小球通过a点后,既可以使小球落到轨道内,也可以使小球落到de面上 |
| C、无论怎样改变h的大小,都不能使小球通过a点后又落回到轨道内 |
| D、使小球通过a点后飞出de面之外(e的右边)是可以通过改变h的大小来实现的 |
 (2009?湛江二模)如图所示,M为固定在桌面上的L形木块,圆槽轨道半径为R,abcd为3/4圆周的光滑轨道,a为轨道的最高点,de面水平且有较长长度.今将质量为m的小球在d点的正上方高h处释放,让其自由下落到d处切入轨道运动.某同学提出以下两个观点:
(2009?湛江二模)如图所示,M为固定在桌面上的L形木块,圆槽轨道半径为R,abcd为3/4圆周的光滑轨道,a为轨道的最高点,de面水平且有较长长度.今将质量为m的小球在d点的正上方高h处释放,让其自由下落到d处切入轨道运动.某同学提出以下两个观点: