题目内容
8. 屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴已刚好到达地面,而第3滴与第2滴分别位于高为1m的窗户的上、下沿(不计水滴大小),如图所示(g取10m/s2),问:
屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴已刚好到达地面,而第3滴与第2滴分别位于高为1m的窗户的上、下沿(不计水滴大小),如图所示(g取10m/s2),问:(1)滴水的时间间隔是多少?
(2)此屋檐离地面多高?
分析 (1)由H=$\frac{1}{2}g{t}^{2}$,得出水从屋檐到地面的时间,从而得出相等的时间间隔.
(2)初速度为0的匀加速直线运动,在连续相等时间间隔内的位移比为1:3:5:7.已知第3滴与第2滴水的间隔距离,根据比例关系求出总高度.
解答 解:(1)根据H=$\frac{1}{2}g{t}^{2}$,代入数据得,t=$\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×3.2}{10}}s=0.8s$
滴水时间间隔$△t=\frac{t}{4}=0.2s$.
(2)根据比例关系,从上到下相邻水滴间距离之比为1:3:5:7,而2、3两滴间距离为1米,所以总高度$H=\frac{1+3+5+7}{5}×1=3.2m$
答:(1)滴水的时间间隔是0.2s;
(2)此屋檐离地面3.2m
点评 解决本题的关键掌握初速度为0的匀加速直线运动,在连续相等时间间隔内的位移比为1:3:5:7.以及掌握自由落体运动的位移时间公式H=$\frac{1}{2}g{t}^{2}$.

练习册系列答案
相关题目
18. 如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )
如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )
 如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )
如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )| A. | 物体A与物体B组成的系统机械能守恒 | |
| B. | 当物体B获得最大速度时,弹簧伸长量为$\frac{2mg}{k}$ | |
| C. | 当物体B获得最大速度时,若弹簧的弹性势能增加量为$\frac{{{m^2}{g^2}}}{2k}$,则物体A的速度大小为$g\sqrt{\frac{m}{2k}}$ | |
| D. | 此过程中B物体机械能的减少量大于弹簧弹性势能的增加量 |
16.火车在平直轨道上匀速行驶,门窗紧闭的车厢内有一人向上跳起,发现仍落回原处的原因是( )
| A. | 人跳起后,车厢内空气给他以向前的推力,带着他随同火车一起向前运动 | |
| B. | 人跳起瞬间,车厢地板给他一向前的推力,推动他随同火车一起向前运动 | |
| C. | 人跳起后,车在继续向前运动,所以人落下后必定偏后一些,只是由于时间很短,偏后的距离不明显? | |
| D. | 人跳起后直到落地,在水平方向上始终和车具有相同的速度 |
13.如图所示,表示物体做匀变速直线运动的是( )


| A. | ①② | B. | ②③ | C. | ①③ | D. | ①④ |
20.面积为5×10-2m2的单匝矩形线圈放在磁感应强度为3×10-2T的匀强磁场中,当线圈平面与磁场方向垂直时,穿过线圈的磁通量是( )
| A. | 3×10-4Wb | B. | 2×10-3Wb | C. | 5×10-2Wb | D. | 1.5×10-3Wb |
17.下列说法符合物理学发展史实的是( )
| A. | 哥白尼发现了行星的运动规律 | |
| B. | 伽利略发现了万有引力定律 | |
| C. | 卡文迪许第一次在实验室里通过“扭秤实验”测出了万有引力常量G | |
| D. | 牛顿提出了日心说 |
18.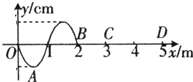 一列简谐横波沿x轴正方向传播,在t=0时波传播到x轴上的质点B,在它左侧的质点A恰好位于负向最大位移处,如图所示,在t=0.6s时,质点A第三次到达正向最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t=0时波传播到x轴上的质点B,在它左侧的质点A恰好位于负向最大位移处,如图所示,在t=0.6s时,质点A第三次到达正向最大位移处,则( )
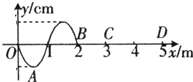 一列简谐横波沿x轴正方向传播,在t=0时波传播到x轴上的质点B,在它左侧的质点A恰好位于负向最大位移处,如图所示,在t=0.6s时,质点A第三次到达正向最大位移处,则( )
一列简谐横波沿x轴正方向传播,在t=0时波传播到x轴上的质点B,在它左侧的质点A恰好位于负向最大位移处,如图所示,在t=0.6s时,质点A第三次到达正向最大位移处,则( )| A. | 该波的速度等于5m/s | |
| B. | t=0.6s时,质点C在平衡位置处且向下运动 | |
| C. | t=0.6s时,质点C在平衡位置处且向上运动 | |
| D. | 当质点D第一次到达正向在最大位移处时,质点B恰好在平衡位置且向下运动 |
 有一个正方形线框的线圈匝数为10匝,边长为20cm,线框总电阻为1Ω,线框绕OO′轴以10πrad/s的角速度匀速转动,如图,垂直于线框平面向里的匀强磁场的磁感应强度为0.5T,求:
有一个正方形线框的线圈匝数为10匝,边长为20cm,线框总电阻为1Ω,线框绕OO′轴以10πrad/s的角速度匀速转动,如图,垂直于线框平面向里的匀强磁场的磁感应强度为0.5T,求: 如图所示,电路中的灯泡标有“0.1V,0.4W”,电源的电动势为4V,内阻为0.05Ω,电动机内阻为0.1Ω,此时灯泡与电动机都正常工作求:
如图所示,电路中的灯泡标有“0.1V,0.4W”,电源的电动势为4V,内阻为0.05Ω,电动机内阻为0.1Ω,此时灯泡与电动机都正常工作求: