题目内容
17. 如图所示,已知半径分别为R和r(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,甲轨道左侧又连接一个光滑的轨道,两圆形轨道之间由一条水平轨道CD相连.一小球自某一高度由静止滑下,先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开圆轨道.若小球在两圆轨道的最高点对轨道压力都恰好为零.试求:
如图所示,已知半径分别为R和r(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,甲轨道左侧又连接一个光滑的轨道,两圆形轨道之间由一条水平轨道CD相连.一小球自某一高度由静止滑下,先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开圆轨道.若小球在两圆轨道的最高点对轨道压力都恰好为零.试求:(1)小球分别经过C、D时的速度VC和VD的大小;
(2)小球由静止释放时的高度h;
(3)水平CD段的长度l.
分析 (1)小球滚到两圆轨道最高点均仅受重力,运用向心力公式可求出在其位置的速度;
(2)因为轨道光滑,则由机械能守恒定律可求出轨道最低点速度,从而也求出释放的高度;
(3)由于CD段粗糙,不能运用机械守恒定律,选用动能定理,就可算出长度.
解答 解:(1)小球在光滑圆轨道上滑行时,机械能守恒,设小球滑过C点时的速度为vc,通过甲环最高点速度为v′,
根据小球对最高点压力为零,有:mg=$\frac{{v}^{′2}}{R}$ ①
取轨道最低点为零势能点,由机械守恒定律得:$\frac{1}{2}$mvC2=mg•2R+$\frac{1}{2}$mv′2 ②
由①、②两式消去v′,可得vC=$\sqrt{5gR}$ ③
同理可得小球滑过D点时的速度vD=$\sqrt{5gr}$ ④
所以小球经过C点的速度为$\sqrt{5gR}$; 经过D点的速度为$\sqrt{5gr}$.
(2)小球从在甲轨道左侧光滑轨道滑至C点时机械能守恒,有:mgh=$\frac{1}{2}$mvC2 ⑤
由③、⑤两式联立解得 h=2.5R
(3)设CD段的长度为l,对小球滑过CD段过程应用动能定理可得:-μmgl=$\frac{1}{2}$mvD2-$\frac{1}{2}$mvC2 ⑥
由③、④、⑥三式联立解得l=$\frac{5(R-r)}{2μ}$
答:(1)小球经过C点的速度为$\sqrt{5gR}$; 经过D点的速度为$\sqrt{5gr}$;
(2)小球由静止释放时的高度为2.5R;
(3)水平CD段的长度为$\frac{5(R-r)}{2μ}$.
点评 掌握向心力公式外,还熟悉了牛顿第二定律,最后比较了机械能守恒定律与动能定理的优缺点.本题中小球在轨道最高点压力为零是解题的切入点.

 质量为m的小球由轻绳a和b分别系于一轻质细杆的A点和B点,如图所示,绳a与水平方向成θ角,绳b在水平方向且长为l,当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )
质量为m的小球由轻绳a和b分别系于一轻质细杆的A点和B点,如图所示,绳a与水平方向成θ角,绳b在水平方向且长为l,当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )| A. | a绳的张力不可能为零 | |
| B. | a绳的张力随角速度的增大而增大 | |
| C. | 当角速度ω>$\frac{g}{tanθ}$,b绳将出现弹力 | |
| D. | 若b绳突然被剪断,则a绳的弹力一定发生变化 |
 已知一足够长的传送带与水平面的倾斜角为θ,以一定的速度匀速运动.某时刻在传送带适当的位置放上具有一定初速度的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2).已知传送带的速度保持不变.(g取10m/s2)则下列判断正确的是( )
已知一足够长的传送带与水平面的倾斜角为θ,以一定的速度匀速运动.某时刻在传送带适当的位置放上具有一定初速度的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2).已知传送带的速度保持不变.(g取10m/s2)则下列判断正确的是( )| A. | 0~t1内,物块对传送带做正功 | |
| B. | 物块与传送带间的动摩擦因数为μ,μ>tanθ | |
| C. | 0~t2内,传送带对物块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| D. | 系统产生的热量一定比物块动能的减少量大 |

 某兴趣小组为了研制一台“电子秤”,找到一个力电转化传感器,该传感器的输出电压正比于受压面的正压力,实验操作时,先调节传感器输入端的电压(要求从零开始调节),使力电转换传感器在空载时的输出电压为零,而后在其受压面上放一物体,即可测得与物体的质量成正比的输出电压.
某兴趣小组为了研制一台“电子秤”,找到一个力电转化传感器,该传感器的输出电压正比于受压面的正压力,实验操作时,先调节传感器输入端的电压(要求从零开始调节),使力电转换传感器在空载时的输出电压为零,而后在其受压面上放一物体,即可测得与物体的质量成正比的输出电压.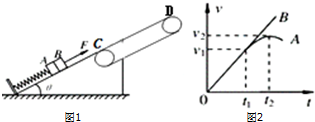

 如图为某工程车的卸货装置,该装置为一能够直接将货物传动到地面的倾角为θ的传送带,该装置在正常工作时传送带匀速传动,传动的速度为v,方向逆时针,卸货工人将质量为m的货物由顶端无初速度放上,已知动摩擦因数为μ,且μ<tanθ,则货物在整个运动过程中的速度随时间变化的规律可能正确的是( )
如图为某工程车的卸货装置,该装置为一能够直接将货物传动到地面的倾角为θ的传送带,该装置在正常工作时传送带匀速传动,传动的速度为v,方向逆时针,卸货工人将质量为m的货物由顶端无初速度放上,已知动摩擦因数为μ,且μ<tanθ,则货物在整个运动过程中的速度随时间变化的规律可能正确的是( )



 海水中含有大量的正、负离子,这些离子随海流做定向运动,如果有磁场能使这些正、负离子向相反方向偏转,便有可能发出电来.如图所示为一利用海流发电的磁流体发电机原理的示意图,上、下两块金属板M、N水平正对放置,浸没在海水里,金属板相距d=100m,在金属板之间加一匀强磁场,磁感应强度大小B=0.05T,方向由南向北,海水从东向西以速度v=5m/s流过两金属板之间,且将在两板之间形成电势差.
海水中含有大量的正、负离子,这些离子随海流做定向运动,如果有磁场能使这些正、负离子向相反方向偏转,便有可能发出电来.如图所示为一利用海流发电的磁流体发电机原理的示意图,上、下两块金属板M、N水平正对放置,浸没在海水里,金属板相距d=100m,在金属板之间加一匀强磁场,磁感应强度大小B=0.05T,方向由南向北,海水从东向西以速度v=5m/s流过两金属板之间,且将在两板之间形成电势差.