题目内容
(2013?黄冈一模)我国的“嫦娥三号”探月卫星将实现“月面软着陆”,该过程的最后阶段是:着陆器离月面h高时速度减小为零,为防止发动机将月面上的尘埃吹起,此时要关掉所有的发动机,让着陆器自由下落着陆.已知地球质量是月球质量的81倍,地球半径是月球半径的4倍,地球半径
=6.4×1
m,地球表面的重力加速度
=10 m/
.不计月球自转的影响(结果保留两位有效数字).
(1)若题中h=3.2m,求着陆器落到月面时的速度大小;
(2)由于引力的作用,月球引力范围内的物体具有引力势能.理论证明,若取离月心无穷远处为引力势能的零势点,距离月心为r的物体的引力势能
=-G
,式中G为万有引力常数,M为月球的质量,m为物体的质量.求着陆器仅依靠惯性从月球表面脱离月球引力范围所需的最小速度.
| R | 0 |
| 0 | 6 |
| g | 0 |
| s | 2 |
(1)若题中h=3.2m,求着陆器落到月面时的速度大小;
(2)由于引力的作用,月球引力范围内的物体具有引力势能.理论证明,若取离月心无穷远处为引力势能的零势点,距离月心为r的物体的引力势能
| E | p |
| Mm |
| r |
分析:(1)着陆器做近似地球表面的自由落体运动,由自由落体规律求解着地速度
(2)着陆器仅依靠惯性从月球表面脱离月球引力范围,根据机械能守恒定律求解初速度
(2)着陆器仅依靠惯性从月球表面脱离月球引力范围,根据机械能守恒定律求解初速度
解答:解:(1)着陆器做近似地球表面的自由落体运动,设着陆器落到月面时的速度大小为v,月球表面物体自由下落加速度为g,故:
v2=2gh①
设月球质量为M,半径为R,忽略月球自转,在月球表面附近质量为m的物体满足:
=mg②
同理,设地球质量为M0,半径为R0,有:
=mg0③
由①②③整理得,v=
=
m/s=3.56m/s
设着陆器至少以速度v0起飞方可冲出月球引力场,则由能量关系得:
-
=0
由①②④并代入数据得:v0=2.5×103m/s
答:(1)着陆器落到月面时的速度大小为3.56m/s
(2)着陆器仅依靠惯性从月球表面脱离月球引力范围所需的最小速度为2.5×103m/s
v2=2gh①
设月球质量为M,半径为R,忽略月球自转,在月球表面附近质量为m的物体满足:
| GMm |
| R2 |
同理,设地球质量为M0,半径为R0,有:
| GM0m | ||
|
由①②③整理得,v=
2g0h
|
2×10×3.2×
|
设着陆器至少以速度v0起飞方可冲出月球引力场,则由能量关系得:
| 1 |
| 2 |
| mv | 2 0 |
| GMm |
| R |
由①②④并代入数据得:v0=2.5×103m/s
答:(1)着陆器落到月面时的速度大小为3.56m/s
(2)着陆器仅依靠惯性从月球表面脱离月球引力范围所需的最小速度为2.5×103m/s
点评:在月球表面的运动类比地球表面的自由落体运动,对于只有保守力做功的情形,注意题应用守恒的观点解决问题

练习册系列答案
相关题目
 (2013?黄冈一模)如图所示,一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为5m,弹丸和砂袋形状大小忽略不计,求两粒弹丸的水平速度之比v0/v为多少?
(2013?黄冈一模)如图所示,一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为5m,弹丸和砂袋形状大小忽略不计,求两粒弹丸的水平速度之比v0/v为多少? (2013?黄冈一模)两端开口、内表面光滑的U形管处于竖直平面内,如图所示,质量均为m=10kg的活塞A、B在外力作用下静止于左右管中同一高度h处,将管内空气封闭,此时管内外空气的压强均为
(2013?黄冈一模)两端开口、内表面光滑的U形管处于竖直平面内,如图所示,质量均为m=10kg的活塞A、B在外力作用下静止于左右管中同一高度h处,将管内空气封闭,此时管内外空气的压强均为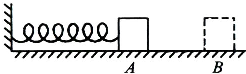 (2013?黄冈一模)如图所示,一轻质弹簧两端分别与竖直墙壁和物块连结,弹簧、地面水平.A、B是物块能保持静止的位置中离墙壁最近和最远的点,A、B两点离墙壁的距离分别是
(2013?黄冈一模)如图所示,一轻质弹簧两端分别与竖直墙壁和物块连结,弹簧、地面水平.A、B是物块能保持静止的位置中离墙壁最近和最远的点,A、B两点离墙壁的距离分别是