题目内容
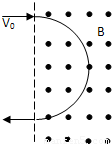 如图所示,一个质子(
如图所示,一个质子(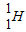 )和一个α粒子(
)和一个α粒子(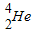 )先后垂直于磁场方向进入同一匀强磁场中,在磁场中的轨道半径相同,经过半个圆周从磁1,3,5场出来.关于它们在磁场中的运动情况,正确的是( )
)先后垂直于磁场方向进入同一匀强磁场中,在磁场中的轨道半径相同,经过半个圆周从磁1,3,5场出来.关于它们在磁场中的运动情况,正确的是( )①质子和α粒子的在磁场中运动的动能相同
②质子和α粒子在磁场中受到的向心力的大小相同
③质子和α粒子在磁场中运动的时间相同
④质子和α粒子在磁场中运动的动量的大小相同.
A.①②
B.①③
C.②④
D.③④
【答案】分析:质子和α粒子进入磁场后做匀速圆周运动,由洛伦兹力提供向心力.质子与α粒子的电量分别为e和2e,质量之比为1:4.推导出轨迹半径与动能、动量的关系,得到周期公式,再进行分析.
解答:解:①由qvB=m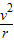 ,动能Ek=
,动能Ek=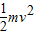 ,得:r=
,得:r=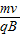 =
=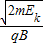
轨道半径r相同,质子与α粒子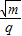 相等,r相等,则得动能Ek相同.故①正确.
相等,r相等,则得动能Ek相同.故①正确.
②在磁场中受到的向心力的大小等于洛伦兹力的大小,公式为F=qvB.由于质子与α粒子的电量分别为e和2e,质量之比为1:4,r相同,由r=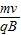 得质子与α粒子的速率之比为2:1
得质子与α粒子的速率之比为2:1
则由F=qvB得知:它们的洛伦兹力相同.故②正确.
③两个粒子在磁场中运动的时间为各自周期的 .周期公式为T=
.周期公式为T=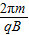 ,与比荷成反比,则得质子与α粒子的周期之比为1:2.故质子和α粒子在磁场中运动的时间不相同.故③错误.
,与比荷成反比,则得质子与α粒子的周期之比为1:2.故质子和α粒子在磁场中运动的时间不相同.故③错误.
④由r=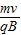 ,动量P=mv,则得P=qBr,r、B相同,q不同,则P不同.故④错误.
,动量P=mv,则得P=qBr,r、B相同,q不同,则P不同.故④错误.
故选A
点评:本题关键要掌握粒子在磁场中圆周运动的半径和周期公式,以及动量、动能等量表达式,结合进行分析.
解答:解:①由qvB=m
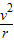 ,动能Ek=
,动能Ek=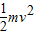 ,得:r=
,得:r=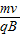 =
=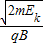
轨道半径r相同,质子与α粒子
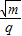 相等,r相等,则得动能Ek相同.故①正确.
相等,r相等,则得动能Ek相同.故①正确.②在磁场中受到的向心力的大小等于洛伦兹力的大小,公式为F=qvB.由于质子与α粒子的电量分别为e和2e,质量之比为1:4,r相同,由r=
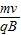 得质子与α粒子的速率之比为2:1
得质子与α粒子的速率之比为2:1则由F=qvB得知:它们的洛伦兹力相同.故②正确.
③两个粒子在磁场中运动的时间为各自周期的
 .周期公式为T=
.周期公式为T=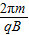 ,与比荷成反比,则得质子与α粒子的周期之比为1:2.故质子和α粒子在磁场中运动的时间不相同.故③错误.
,与比荷成反比,则得质子与α粒子的周期之比为1:2.故质子和α粒子在磁场中运动的时间不相同.故③错误.④由r=
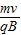 ,动量P=mv,则得P=qBr,r、B相同,q不同,则P不同.故④错误.
,动量P=mv,则得P=qBr,r、B相同,q不同,则P不同.故④错误.故选A
点评:本题关键要掌握粒子在磁场中圆周运动的半径和周期公式,以及动量、动能等量表达式,结合进行分析.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图所示,一个质子和一个α粒子先后垂直磁场方向进入一个有理想边界的匀强磁场区域,它们在磁场中的运动轨迹完全相同,都是以图中的O点为圆心的半圆.已知质子与α粒子的电荷量之比q1:q2=1:2,质量之比m1:m2=1:4,则以下说法中正确的是( )
如图所示,一个质子和一个α粒子先后垂直磁场方向进入一个有理想边界的匀强磁场区域,它们在磁场中的运动轨迹完全相同,都是以图中的O点为圆心的半圆.已知质子与α粒子的电荷量之比q1:q2=1:2,质量之比m1:m2=1:4,则以下说法中正确的是( )| A、它们在磁场中运动时的动能相等 | B、它们在磁场中所受到的向心力大小相等 | C、它们在磁场中运动的时间相等 | D、它们在磁场中运动时的动量大小相等 |
 如图所示,一个质子(
如图所示,一个质子( 如图所示,一个质子的电量e=1.6×10-19C,在某一静电场中从A点经C点移到B点,电场力做功8×10-17J;在质子从B点经D点回到A 点过程中,电场力做功为
如图所示,一个质子的电量e=1.6×10-19C,在某一静电场中从A点经C点移到B点,电场力做功8×10-17J;在质子从B点经D点回到A 点过程中,电场力做功为 如图所示,一个质子沿着逆时针的方向做匀速圆周运动,则做此运动的质子( )
如图所示,一个质子沿着逆时针的方向做匀速圆周运动,则做此运动的质子( ) 如图所示,一个质子沿abc的轨迹运动,则( )
如图所示,一个质子沿abc的轨迹运动,则( )