题目内容
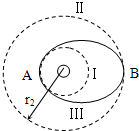我国“神舟六号”宇宙飞船的成功发射和回收，标志着我国的航天技术已达到世界先进水平．如图所示，质量为m的飞船绕地球在圆轨道I上运行时，半径为r1，要进入半径为r2的更高圆轨道Ⅱ，必须先加速进入一个椭圆轨道Ⅲ，然后再进入圆轨道Ⅱ．已知飞船在圆轨道Ⅱ上运动的速度大小为v，在A点通过发动机向后喷出一定质量气体，使飞船速度增加到v’进入椭圆轨道Ⅲ．求飞船在轨道I上的速度和加速度大小．分析：根据万有引力提供向心力结合轨道半径的关系求出线速度的大小，根据向心加速度的公式求出向心加速度的大小．
解答：解：在轨道Ⅰ上，有G
=m
，得v1=
．
同理在轨道Ⅱ上，v=
．
联立得，v1=v
．
设在轨道Ⅰ上的向心加速度为a1，则a1=
将v1=v
代入上式，解得a1=
v2．
答：飞船在轨道I上的速度为v1=v
，加速度大小a1=
v2．
| Mm |
| r12 |
| v12 |
| r1 |
|
同理在轨道Ⅱ上，v=
|
联立得，v1=v
|
设在轨道Ⅰ上的向心加速度为a1，则a1=
| v12 |
| r1 |
将v1=v
|
| r2 |
| r12 |
答：飞船在轨道I上的速度为v1=v
|
| r2 |
| r12 |
点评：解决本题的关键掌握万有引力提供向心力这一理论，并能熟练运用．
练习册系列答案
智能训练练测考系列答案
相关题目
四圈，依次飞经中国和太平洋地区的四次轨迹①、②、③、④，图中分别标出了各地点的经纬
度（如：在轨迹①通过赤道时的经度为西经156°，绕行一圈后轨迹②再次经过赤道时经度为180°，……），若已知地球半径为R，地球表面处的重力加速度g，地球自转周期为24h，根据图中的信息：
示
，试写出飞船离地面高度的表达式。