题目内容
如图所示，长L=75cm的质量m=2kg的平底玻璃管底部置有一玻璃小球，玻璃管从静止开始受到一竖直向下的恒力F=12N的作用，使玻璃管竖直向下运动，经一段时间t，小球离开管口．空气阻力不计，取g=10m/s2．求：时间t和小球离开玻璃管时玻璃管的速度的大小．
【答案】分析：设玻璃管向下运动的加速度为a，对玻璃管受力分析由牛顿第二定律列式，玻璃球作自由落体运动，玻璃管向下加速运动，根据运动学基本公式列式，再抓住位移关系列式，联立方程组即可求解．
解答：解：设玻璃管向下运动的加速度为a，对玻璃管受力分析由牛顿第二定律得，F+mg=ma①
设玻璃球和玻璃管向下运动的位移分别为s1、s2时，玻璃球离开玻璃管，
由题意得，s2-s1=L②
由玻璃球作自由落体运动得，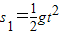
③
由玻璃管向下加速运动得，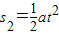
④
玻璃球离开玻璃管时，玻璃管的速度v=at⑤
由①～⑤式解得，t=0.5s，v=8m/s．
答：时间t为0.5s，小球离开玻璃管时玻璃管的速度的大小为8m/s．
点评：本题主要考查了牛顿第二定律及运动学基本公式的应用，难度不大，属于基础题．
解答：解：设玻璃管向下运动的加速度为a，对玻璃管受力分析由牛顿第二定律得，F+mg=ma①
设玻璃球和玻璃管向下运动的位移分别为s1、s2时，玻璃球离开玻璃管，
由题意得，s2-s1=L②
由玻璃球作自由落体运动得，
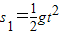③由玻璃管向下加速运动得，
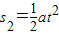④玻璃球离开玻璃管时，玻璃管的速度v=at⑤
由①～⑤式解得，t=0.5s，v=8m/s．
答：时间t为0.5s，小球离开玻璃管时玻璃管的速度的大小为8m/s．
点评：本题主要考查了牛顿第二定律及运动学基本公式的应用，难度不大，属于基础题．
练习册系列答案
相关题目
