题目内容
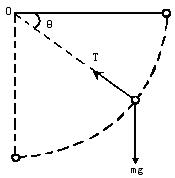
绳一端连着一质量为m的小球，另一端悬挂于O点．现将绳拉直，球从与悬点等高处由静止释放，求球运动过程中速度的竖直分量最大时的位置(即悬线与水平方向的夹角)．
答案：
解析：
提示：
解析：
|
球做变速圆周运动，竖直方向先加速后减速，竖直方向的合外力先向下后向上．竖直方向的合力为0时，竖直分速vy最大.设绳转过θ角时，vy最大，此时设球速为v．由机械能守恒得
mgLsinθ= 此时小球受绳的张力T和重力G，由四周运动规律得
T－mgLsinθ＝ 得 T＝3mgsinθ， 此时竖直方向合力为零，如图所示有 Tsinθ＝mg， 联立解得：
sinθ＝
|
mv2，
，
．
提示：
|
变速圆周运动某时刻的速度与该位置的沿半径方向的合力具有瞬时对应关系．竖直分速度最大时，该时刻竖直方向合力为零． |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
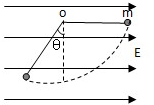两平行板间有水平匀强电场，一根长为L=0.1m，不可伸长的不导电细绳的一端连着一个质量为 m=0.1g、带电量为q=5x10-6C的小球，另一端固定于O点．把小球拉起直至细线与电场线平行，然后无初速度释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ=37°求
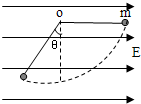两平行板间有水平匀强电场，一根长为L，不可伸长的不导电细绳的一端连着一个质量为 m、带电量为q的小球，另一端固定于O点．把小球拉起直至细线与电场线平行，然后无初速度释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ=30°求：
