题目内容
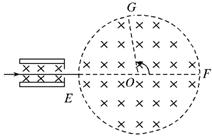
图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁感应强度大小为B0,方向与金属板面平行并垂直于纸面向里,图中右边有一半径为R､圆心为O的圆形区域,区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向里.一电荷量为q的正离子沿平行于金属板面､垂直于磁场的方向射入平行金属板之间,沿同一方向射出平行金属板之间的区域,并沿直径EF方向射入磁场区域,最后从圆形区域边界上的G点射出.已知弧
所对应的圆心角为θ.不计重力.求
(1)离子速度的大小;
(2)离子的质量.
(1)
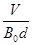(2)
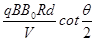
【解析】本题考查牛顿第二定律及粒子在磁场中的运动等知识.
(1)由题设知,离子在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,qvB0=qE0 ①
式中,v是离子运动速度的大小,E0是平行金属板之间的匀强电场的强度,因此有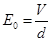
②
由①②式得
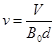. ③
(2)在圆形磁场区域,离子做匀速圆周运动,由洛伦兹力公式和牛顿第二定律有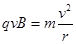
④
式中,m和r分别是离子的质量和它做圆周运动的半径.由题设,离子从磁场分界上的点G穿出,离子运动的圆周的圆心O′必在过E点垂直于EF的直线上,且在EG的垂直平分线上(如图).由几何关系有r=Rtanα ⑤
式中,α是OO′与直径EF的夹角.由几何关系有2α+θ=π ⑥
联立③④⑤⑥式得,离子的质量为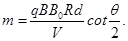
培优好卷单元加期末卷系列答案
如图中左边有一对平行金属板，两板间有相互垂直的电场和磁场，向下的匀强电场强度大小为E、垂直向里的匀强磁场磁感应强度大小为B1．图中右边有一半径为R、圆心为O的圆形区域内存在匀强磁场，磁感应强度大小为B2，方向垂直于纸面朝里．一电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入平行金属板之间，沿同一方向射出平行金属板之间的区域，并沿直径CD方向射入圆形磁场区域，最后从圆形区城边界上的P点射出．已知半径OD、OP的夹角θ，不计重力．求
（2010?海南）图中左边有一对平行金属板，两板相距为d．电压为V；两板之间有匀强磁场，磁感应强度大小为B0，方向与金属板面平行并垂直于纸面朝里．图中右边有一半径为R、圆心为O的圆形区域内也存在匀强磁场，磁感应强度大小为B，方向垂直于纸面朝里．一电荷量为q的正离子沿平行于全属板面、垂直于磁场的方向射入平行金属板之间，沿同一方向射出平行金属板之间的区域，并沿直径EF方向射入磁场区域，最后从圆形区城边界上的G点射出．已知弧
图中左边有一对平行金属板，两板相距为d，电压为V；两板之间有匀强磁场，磁感应强度大小为B0，方向平行于板面并垂直于纸面朝里．图中右边有一边长为a的正三角形区域EFG（EF边与金属板垂直），在此区域内及其边界上也有匀强磁场，磁感应强度大小为B，方向垂直于纸面朝里．假设一系列电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入金属板之间，沿同一方向射出金属板之间的区域，并经EF边中点H射入磁场区域．不计重力．
如图所示，图中左边有一对平行金属板，两板相距为d，电压为U．两板之间有匀强磁场，磁感应强度大小为B0，方向与金属板面平行并垂直于纸面朝里；图中右边有一半径为R、圆心为O的圆形区域，区域内也存在匀强磁场，磁感应强度大小为B，方向垂直于纸面朝里．一电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入平行金属板之间，沿同一方向射出平行金属板之间的区域，并沿直径PQ方向射入磁场区域，最后从圆形区域边界上的G点射出，已知弧QG所对应的圆心角为θ．离子重力不计．求：
图中左边有一对平行金属板，两板相距为d，电压为V;两板之间有匀强磁场，磁场应强度大小为B0，方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直)，在此区域内及其边界上也有匀强磁场，磁感应强度大小为B，方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面，垂直于磁场的方向射入金属板之间，沿同一方向射出金属板之间的区域，并经EF边中点H射入磁场区域。不计重力
，求离子乙的质量。（3）若这些离子中的最轻离子的质量等于离子甲质量的一半，而离子乙的质量是最大的，问磁场边界上什么区域内可能有离子到达。