题目内容
1. 两物块A、B用轻弹簧相连,质量均为3kg,初始时弹簧处于原长,A、B两物块都以v=4m/s的速度在光滑的水平地面上向右运动,质量为2kg的物块C静止在前方,如图所示.B与C碰撞后二者会粘在一起运动.求:
两物块A、B用轻弹簧相连,质量均为3kg,初始时弹簧处于原长,A、B两物块都以v=4m/s的速度在光滑的水平地面上向右运动,质量为2kg的物块C静止在前方,如图所示.B与C碰撞后二者会粘在一起运动.求:(1)B与C碰撞后瞬间B与C的速度;
(2)当弹簧的弹性势能最大时,物块A的速度为多大.
分析 (1)B与C发生碰撞后,B的速度减小,BC一起向右运动.并碰撞过程由动量守恒定律可求得碰后BC的速度;
(2)对整体分析,由动量守恒定律可求得最后ABC三者共同的速度.
解答 解:①设向右为正方向;
对BC碰撞过程:
mBv=(mB+mC)vBC
即 vBC=2.4m/s
②当ABC三者达到共同速度时,弹簧压缩到最短,对ABC组成的系统,由动量守恒
(mA+mB)v=(mA+mB+mC)VABC
即 VABC=3m/s
答:(1)B与C碰撞后瞬间B与C的速度为2.4m/s;
(2)当弹簧的弹性势能最大时,物块A的速度为3m/s.
点评 本题考查动量守恒定律的应用,在解题时要注意正确选择研究对象,明确是哪一系统能应用动量守恒.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.一个原子核${\;}_{92}^{235}$U在中子的轰击下发生一种可能的裂变反应,其裂变方程为${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→X+${\;}_{38}^{94}$Sr+2${\;}_{0}^{1}$n,则下列叙述正确的是( )
| A. | X原子核中含有140个核子 | |
| B. | X原子核中含有86个中子 | |
| C. | 因为裂变时释放能量,所以裂变后粒子的总质量数增加 | |
| D. | 因为裂变时释放能量,所以裂变后粒子的总质量数减少 | |
| E. | 因为裂变时释放能量,所以裂变后粒子的总质量减少 |
9. 如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )
如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )
 如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )
如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,则下列说法正确的是( )| A. | 物体所受弹力增大,摩擦力也增大 | B. | 物体所受弹力增大,摩擦力不变 | ||
| C. | 物体所受弹力增大,摩擦力减小 | D. | 物体所受弹力减小,摩擦力也减小 |
16. 氦原子被电离一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为E1=-54.4eV,氦离子能级的示意图如图所示.在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是( )
氦原子被电离一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为E1=-54.4eV,氦离子能级的示意图如图所示.在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是( )
 氦原子被电离一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为E1=-54.4eV,氦离子能级的示意图如图所示.在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是( )
氦原子被电离一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为E1=-54.4eV,氦离子能级的示意图如图所示.在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是( )| A. | 54.4eV | B. | 51.0eV | C. | 43.2eV | D. | 40.8eV |
6. 如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
 如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )
如图所示,将a、b两小球以大小均为10$\sqrt{6}$m/s的初速度分别从A、B两点相差1s先后水平相向抛出(A点比B点高),a小球从A点抛出后,经过时间t,a、b两小球恰好在空中相遇,此时速度方向相互垂直,不计空气阻力,取g=10m/s2.则从a小球抛出到两小球相遇,小球a下落的时间t和高度h分别是( )| A. | t=2s | B. | t=3s | C. | h=45 m | D. | h=20 m |
13.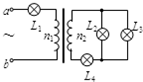 如图所示为理想变压器,三个灯泡L1、L2、L3都标有“4V,4W”,灯泡L4标有“4V,8W”,若它们都能正常发光,则变压器原、副线圈匝数比n1:n2和ab间输入电压为( )
如图所示为理想变压器,三个灯泡L1、L2、L3都标有“4V,4W”,灯泡L4标有“4V,8W”,若它们都能正常发光,则变压器原、副线圈匝数比n1:n2和ab间输入电压为( )
 如图所示为理想变压器,三个灯泡L1、L2、L3都标有“4V,4W”,灯泡L4标有“4V,8W”,若它们都能正常发光,则变压器原、副线圈匝数比n1:n2和ab间输入电压为( )
如图所示为理想变压器,三个灯泡L1、L2、L3都标有“4V,4W”,灯泡L4标有“4V,8W”,若它们都能正常发光,则变压器原、副线圈匝数比n1:n2和ab间输入电压为( )| A. | 2:1,16V | B. | 2:1,20V | C. | 1:2,16V | D. | 1:2,20V |
10. 如图所示为理想LC振荡回路,某时刻电容器极板间的场强方向和线圈中的磁场方向如图,下列哪些说法是正确的( )
如图所示为理想LC振荡回路,某时刻电容器极板间的场强方向和线圈中的磁场方向如图,下列哪些说法是正确的( )
 如图所示为理想LC振荡回路,某时刻电容器极板间的场强方向和线圈中的磁场方向如图,下列哪些说法是正确的( )
如图所示为理想LC振荡回路,某时刻电容器极板间的场强方向和线圈中的磁场方向如图,下列哪些说法是正确的( )| A. | 此时电容器正在放电 | |
| B. | 此时线圈中的磁场能在增加 | |
| C. | 若在线圈中插入铁芯,振荡电流的频率增大 | |
| D. | 若增大电容器极板间距,振荡电流的频率增大 |
11. 如图,将一质点从放置在粗糙水平地面上的光滑半圆型槽的槽口A点由静止释放,经最低点B运动到与A等高的C点,半圆型槽未发生移动.下列说法正确的是( )
如图,将一质点从放置在粗糙水平地面上的光滑半圆型槽的槽口A点由静止释放,经最低点B运动到与A等高的C点,半圆型槽未发生移动.下列说法正确的是( )
 如图,将一质点从放置在粗糙水平地面上的光滑半圆型槽的槽口A点由静止释放,经最低点B运动到与A等高的C点,半圆型槽未发生移动.下列说法正确的是( )
如图,将一质点从放置在粗糙水平地面上的光滑半圆型槽的槽口A点由静止释放,经最低点B运动到与A等高的C点,半圆型槽未发生移动.下列说法正确的是( )| A. | 从A到C,半圆型槽所受摩擦力先增大再减小 | |
| B. | 从A到C,半圆型槽所受摩擦力的方向先向左再向右 | |
| C. | 从A到B,质点所受重力的瞬时功率先增大后减小 | |
| D. | 从B到C,质点所受弹力的瞬时功率不断减小 |
 小球A和小球B位于同一竖直线上,相距为L,小球B离水平地面高度为h,两球同时由静止释放,如图所示.球A的质量为m,球B的质量为2m.设所有碰撞都是弹性碰撞,重力加速度大小为g,忽略球的直径、空气阻力及碰撞时间.
小球A和小球B位于同一竖直线上,相距为L,小球B离水平地面高度为h,两球同时由静止释放,如图所示.球A的质量为m,球B的质量为2m.设所有碰撞都是弹性碰撞,重力加速度大小为g,忽略球的直径、空气阻力及碰撞时间.