题目内容
 如图所示,A.B为两个靠得很近的小球,均可视为质点,静止放于倾角为θ的光滑斜面上,斜面足够长,在释放B 球的同时,将A球以初速度v0水平抛出,当A球落于斜面上的P点时,求此时A球与B球的间距大小(重力加速度为g).
如图所示,A.B为两个靠得很近的小球,均可视为质点,静止放于倾角为θ的光滑斜面上,斜面足够长,在释放B 球的同时,将A球以初速度v0水平抛出,当A球落于斜面上的P点时,求此时A球与B球的间距大小(重力加速度为g).分析:A球做平抛运动,抓住水平位移和竖直位移的关系,求出运动的时间,从而求出落在斜面上时AP的距离,根据牛顿第二定律求出B球的加速度,结合匀变速直线运动的公式求出B球的位移,从而得出两球的间距.
解答:解:对A:tanθ=
=
=
解得t=
则水平位移x=v0t=
sA=
=
.
对B:根据牛顿第二定律得,a=
=gsinθ
sB=
at2=
△S=SA-SB=
.
答:此时A球与B球的间距大小为
.
| y |
| x |
| ||
| v0t |
| gt |
| 2v0 |
解得t=
| 2v0tanθ |
| g |
则水平位移x=v0t=
| 2v02tanθ |
| g |
sA=
| x |
| cosθ |
| 2v02sinθ |
| gcos2θ |
对B:根据牛顿第二定律得,a=
| mgsinθ |
| m |
sB=
| 1 |
| 2 |
| 2v02sin3θ |
| gcos2θ |
△S=SA-SB=
| 2v02sin3θ |
| g |
答:此时A球与B球的间距大小为
| 2v02sin3θ |
| g |
点评:解决本题的关键掌握平抛运动在水平方向上和竖直方向上的运动规律,抓住竖直位移和水平位移的关系得出运动的时间.

练习册系列答案
相关题目
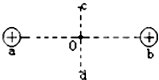 如图所示,a、b为两个固定的带等量正电荷的点电荷,虚线ab、cd互相垂直平分,负电荷q由c点从静止释放,如果只受电场力作用,则下列关于此电荷运动的说法正确的是( )
如图所示,a、b为两个固定的带等量正电荷的点电荷,虚线ab、cd互相垂直平分,负电荷q由c点从静止释放,如果只受电场力作用,则下列关于此电荷运动的说法正确的是( )| A、从c到d电势先减小后增大 | B、在cd间做往复运动,经O点时速度最大 | C、从c到O加速度减小,从O到d加速度增大 | D、运动过程中动能与电势能总量不变 |
 如图所示,A、B为两个用绝缘细线悬挂起来的质量相同的带电介质小球,左边放一个带正电的球C时,两悬线都保持竖直方向(两线长度相同).若把C球移走,两球没有发生接触,那么下面四个图中,哪个图可以正确表示A、B两球的位置( )
如图所示,A、B为两个用绝缘细线悬挂起来的质量相同的带电介质小球,左边放一个带正电的球C时,两悬线都保持竖直方向(两线长度相同).若把C球移走,两球没有发生接触,那么下面四个图中,哪个图可以正确表示A、B两球的位置( ) 如图所示,A、B为两个固定的等量的同种正电荷,在它们连线的中点处有一个可以自由运动的正电荷C,现给电荷C一个垂直于连线的初速度v0,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )
如图所示,A、B为两个固定的等量的同种正电荷,在它们连线的中点处有一个可以自由运动的正电荷C,现给电荷C一个垂直于连线的初速度v0,若不计电荷C所受的重力,则关于电荷C运动过程中的速度和加速度情况,下列说法正确的是( )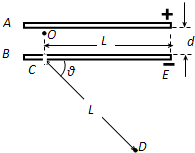 如图所示,A、B为两块平行金属板,A板带正电、B板带负电.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开小孔C.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电粒子(粒子的重力不计),问:
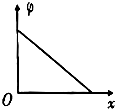
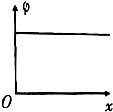
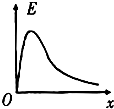
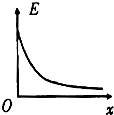
如图所示,A、B为两块平行金属板,A板带正电、B板带负电.两板之间存在着匀强电场,两板间距为d、电势差为U,在B板上开小孔C.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电粒子(粒子的重力不计),问: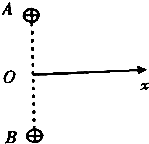 如图所示,A、B为两个等量正点电荷,D为A、B连线的中点.以O为坐标原点、垂直AB向右为正方向建立Ox轴.下列四幅图分别反映了在x轴上各点的电势φ(取无穷远处电势为零)和电场强度E的大小随坐标x的变化关系,其中正确的是( )
如图所示,A、B为两个等量正点电荷,D为A、B连线的中点.以O为坐标原点、垂直AB向右为正方向建立Ox轴.下列四幅图分别反映了在x轴上各点的电势φ(取无穷远处电势为零)和电场强度E的大小随坐标x的变化关系,其中正确的是( )