题目内容
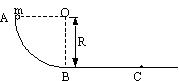
是竖直平面内的四分之一圆弧轨道，在下端B与水平直轨道相切，如图所示。一小球自A点起由静止开始沿轨道下滑。已知圆轨道半径为R，小球的质量为m，不计各处摩擦。求
（1）小球运动到B点时的动能
（2）小球下滑到距水平轨道的高度为R时的速度大小和方向
（3）小球经过圆弧轨道的B点和水平轨道的C点时，所受轨道支持力NB、NC各是多大？
答案：
解析：
解析：
（1）根据机械能守恒 Ek=mgR （2）根据机械能守恒 ΔEk=ΔEp mv2=mgR 小球速度大小v= 速度方向沿圆弧的切线向下，与竖直方向成30° （3）根据牛顿运动定律及机械能守恒，在B点 NB－mg=m ,mgR＝mvB2 解得 NB=3mg 在C点：NC=mg |
练习册系列答案
步步高达标卷系列答案
相关题目
AB是竖直平面内的四分之一圆弧轨道，在下端B与水平直轨道相切，如图所示．一小球自A点起由静止开始沿轨道下滑．已知圆轨道半径为R，小球的质量为m，不计各处摩擦．求：
AB是竖直平面内的四分之一圆弧轨道，在下端B与水平直轨道相切，如图所示．一小球自A点起由静止开始沿轨道下滑．已知圆轨道半径为R，小球的质量为m，不计各处摩擦．求：
如图所示，
知圆轨道半径为R=0.20m，小球的质量为m=0.05kg，不计各处摩擦．求：（取g=10m/s2）
如图所示，AB是竖直平面内的四分之一光滑圆弧，O为圆心，OA水平．一质量m=1kg的小球自圆弧上的A点由静止释放后沿圆弧运动到B点，离开B点后做平抛运动，最终落在地面上的C点，已知B点离地面的高度h=0.8m，BC间的水平距离s=2m，g=10m/s2，求