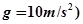题目内容
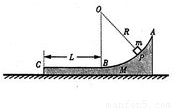
一工件置于水平地面上,其AB段为一半径R=1.0 m的光滑圆弧轨道,BC段为一长度L=0.5 m的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2 kg,与B、C间的动摩擦因数μ1=0.4.工件质量M=0.8 kg,与地面间的动摩擦因数μ2=0.1.(取g=10 m/s2)

(1)若工件固定,将物块由P点无初速度释放,滑至C点时恰好静止,求P、C两点间的高度差h;
(2)若将一水平恒力F作用于工件,使物块在P点与工件保持相对静止,一起向左做匀加速直线运动,求F的大小
【答案】
(1)0.2 m(2)8.5 N
【解析】
试题分析:(1)物块从P点下滑经B点至C点的整个过程,根据动能定理得:
mgh-μ1mgL=0 ① 2分
代入数据得:h=0.2 m. ② 1分
(2)①设物块的加速度大小为a,P点与圆心的连线与竖直方向间的夹角为θ,由几何关系可得:
cos θ=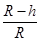 ③ 1分
③ 1分
根据牛顿第二定律,对物块有:mgtan θ=ma ④ 2分
对工件和物块整体有:F-μ2(M+m)g=(M+m)a ⑤ 2分
联立②③④⑤式,代入数据得:F=8.5 N. ⑥ 1分。
考点:本题考查动能定理与牛顿第二定律。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
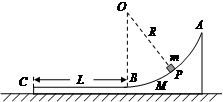 如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数μ1=0.4.工件质量M=0.8kg,与地面间的动摩擦因数μ2=0.1.(取g=10m/s2)
如图所示,一工件置于水平地面上,其AB段为一半径R=1.0m的光滑圆弧轨道,BC段为一长度L=0.5m的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量m=0.2kg,与BC间的动摩擦因数μ1=0.4.工件质量M=0.8kg,与地面间的动摩擦因数μ2=0.1.(取g=10m/s2) 的光滑圆弧轨道,BC段为一长度
的光滑圆弧轨道,BC段为一长度 的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量
的粗糙水平轨道,二者相切于B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点.一可视为质点的物块,其质量 ,与BC间的动摩擦因数
,与BC间的动摩擦因数 .工件质量
.工件质量 ,与地面间的动摩擦因数
,与地面间的动摩擦因数 .(取
.(取 )
)
 .
. 作用于工件,使物块在P点与工件保持相对静止,一起向左做匀加速直线运动.
作用于工件,使物块在P点与工件保持相对静止,一起向左做匀加速直线运动. 时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离.
时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离. 0.4。工件质量M=0.8kg,与地面间的动摩擦因数
0.4。工件质量M=0.8kg,与地面间的动摩擦因数 。(取g=10m/s2)
。(取g=10m/s2)
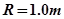 的光滑圆弧轨道,BC段为一长度
的光滑圆弧轨道,BC段为一长度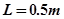 的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点。一可视为质点的物块,其质量
的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点。一可视为质点的物块,其质量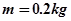 ,与BC间的动摩擦因数
,与BC间的动摩擦因数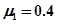 。工件质
。工件质 ,与地面间的动摩擦因数
,与地面间的动摩擦因数 。(取
。(取