题目内容
光滑水平面上有一质量为M、长度为L的木板AB,在木板的中点有一质量为m的小木块,木板上表面是粗糙的,它与木块间的动摩擦因数为μ.开始时两者均处于静止状态,现在木板的B端加一个水平向右的恒力F,则:

1.木板和木块运动的加速度是多大?
2.若在木板的B端到达距右方距离为L的P点前,木块能从本板上滑出,则水平向右的恒力F应满足什么条件?
【答案】
1.
2.
【解析】(1)(5分)木块运动的最大加速度为 ①
①
若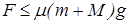 ,木板和木块一起做匀加速运动,根据牛顿第二定律,共同加速度为
,木板和木块一起做匀加速运动,根据牛顿第二定律,共同加速度为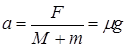 ②
②
若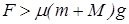 ,设木块、木板加速度分别为
,设木块、木板加速度分别为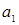 、
、 ,则
,则
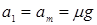 ③
③
 ④
④
(2)(5分)设在木板的B端到达距右方距离为L的P点时,木块恰能从木板上滑出,相对滑动时间为t,水平向右的恒力 ,则
,则
 ⑤
⑤
 ⑥
⑥
由③④⑤⑥式得
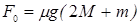 ⑦
⑦
则在木板的B端到达距右方距离为L的P点前,木块能从木板上滑出应满足
 ⑧
⑧

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
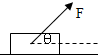 如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )
如图,在光滑水平面上有一质量为m的物体,在与水平方向成θ角的恒定拉力F作用下运动,则在时间t内( )| A、重力的冲量为0 | B、拉力F的冲量为Ft | C、拉力F的冲量为Ftcosθ | D、拉力F的冲量等于物体动量的变化量 |
 如图所示,光滑水平面上有一质量M=1.0kg的小车,小车右端有一个质量m=0.90kg的滑块,滑块与小车左端的挡板之间用轻弹簧相连接,滑块与车面间的动摩擦因数μ=0.20,车和滑块一起以v1=10m/s的速度向右做匀速直线运动,此时弹簧为原长.一质量m0=0.10kg的子弹,以v0=50m/s的速度水平向左射入滑块而没有穿出,子弹射入滑块的时间极短.当弹簧压缩到最短时,弹簧被锁定(弹簧在弹性限度内),测得此时弹簧的压缩量d=0.50m,重力加速度g=10m/s2,求:
如图所示,光滑水平面上有一质量M=1.0kg的小车,小车右端有一个质量m=0.90kg的滑块,滑块与小车左端的挡板之间用轻弹簧相连接,滑块与车面间的动摩擦因数μ=0.20,车和滑块一起以v1=10m/s的速度向右做匀速直线运动,此时弹簧为原长.一质量m0=0.10kg的子弹,以v0=50m/s的速度水平向左射入滑块而没有穿出,子弹射入滑块的时间极短.当弹簧压缩到最短时,弹簧被锁定(弹簧在弹性限度内),测得此时弹簧的压缩量d=0.50m,重力加速度g=10m/s2,求: 光滑水平面上有一质量为M的木板,在木板的最左端有一质量为m的小滑块(可视为质点).小滑块与木板之间的动摩擦因数为μ.开始时它们都处于静止状态,某时刻给小滑块一瞬时冲量,使小滑块以初速度v0向右运动.经过一段时间小滑块与木板达到共同速度v,此时小滑块与木板最左端的距离为d,木板的位移为x,如图所示.下列关系式正确的是( )
光滑水平面上有一质量为M的木板,在木板的最左端有一质量为m的小滑块(可视为质点).小滑块与木板之间的动摩擦因数为μ.开始时它们都处于静止状态,某时刻给小滑块一瞬时冲量,使小滑块以初速度v0向右运动.经过一段时间小滑块与木板达到共同速度v,此时小滑块与木板最左端的距离为d,木板的位移为x,如图所示.下列关系式正确的是( ) 光滑水平面上有一质量为M滑块,滑块的左侧是一光滑的
光滑水平面上有一质量为M滑块,滑块的左侧是一光滑的 如图所示,光滑水平面上有一质量为M、长为L的长木板,其上有一质量为m的物块,它与长木板间的动摩擦因数为μ,开始时长木板与小物块均靠在与水平面垂直的左边固定挡板处以共同的速度v0向右运动,当长木板与右边固定竖直挡板碰撞后立即以大小相同的速率反向运动,且左右挡板之间的距离足够长.
如图所示,光滑水平面上有一质量为M、长为L的长木板,其上有一质量为m的物块,它与长木板间的动摩擦因数为μ,开始时长木板与小物块均靠在与水平面垂直的左边固定挡板处以共同的速度v0向右运动,当长木板与右边固定竖直挡板碰撞后立即以大小相同的速率反向运动,且左右挡板之间的距离足够长.