题目内容
如图所示在xoy所在的平面内，有两根金属丝MN和PQ，其形状分别满足方程y=asin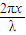
和y=-asin
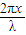，在两金属丝端点从M、P和N、Q之间各接二阻值为A的电阻丝，中间三个相交处均有绝缘表面层相隔，金属丝电阻不计．x＜0的区域内存在垂直xoy平面向下的磁感应强度为B的匀强磁场．两金属丝在沿x轴负方向的外力作用下，以初速度v匀速进入磁场．（1）用法拉第电磁感应定律证明，金属丝上的感应电流是正弦式电流．
（2）求将两金属丝全部拉入磁场中，外力所做的功．
（3）假设仅在
＜x＜0的区域内存在垂xoy平面向下的磁感应强度为B的匀强磁场，求将两金属丝以速度v匀速拉过磁场外力所做的功．
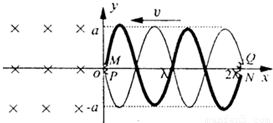
【答案】分析：（1）根据法拉第电磁感应定律表示出感应电动势e的大小，再由欧姆定律得到感应电流的大小表达式．即可证明．
（2）由上题结果可知金属丝中感应电流的最大值Im，可求得有效值I=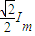
，根据焦耳定律求两电阻丝的发热量，根据能量守恒得知，线框匀速运动时外力所做的功等于总热量．
（3）先求出两金属丝拉入或拉出磁场时，感应电动势的最大值，得到有效值，根据焦耳定律求得外力做功；再用同样的方法求出线框通过磁场时外力做功，即可求得外力所做的总功．
解答：解：（1）在t-t+△t时间间隔内
△Φt=BLv△t=B?2asin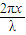
?v△t=2Bavsin
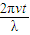△t
据法拉第电磁感应定律E=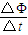
得
e=2Bavsin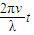
感应电流i=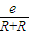
=
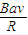sin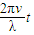
可见金属丝上的感应电流是正弦式电流．证毕．
（2）由上知：感应电流的最大值Im=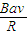
，有效值为I=
=
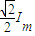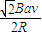
根据功能关系得：W=Q=I2R总t=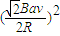
?（2R）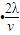
=
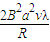
（3）①将两金属丝拉入或拉出磁场区域的过程中，感应电动势最大值为
Em1=2Bav
感应电流最大值 Im1=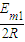
=
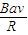
拉力做功 W1=Q1=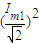
=
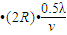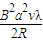
②拉金属丝穿过磁场区域的过程中，感应电动势最大值为Em2=4Bav
感应电流最大值 Im2=2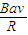
拉力做功 W2=Q2=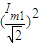
?（2R）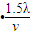
=
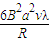
故将两金属丝以速度v匀速拉过磁场外力所做的功为
W′=2W1+W2=2?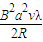
+
=
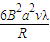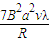
答：
（1）证明略．
（2）将两金属丝全部拉入磁场中，外力所做的功为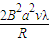
．
（3）将两金属丝以速度v匀速拉过磁场外力所做的功为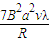
．
点评：本题关键是运用法拉第定律得到感应电流的表达式，判断出产生了正弦式电流，求电功时应用有效值．
（2）由上题结果可知金属丝中感应电流的最大值Im，可求得有效值I=
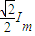，根据焦耳定律求两电阻丝的发热量，根据能量守恒得知，线框匀速运动时外力所做的功等于总热量．（3）先求出两金属丝拉入或拉出磁场时，感应电动势的最大值，得到有效值，根据焦耳定律求得外力做功；再用同样的方法求出线框通过磁场时外力做功，即可求得外力所做的总功．
解答：解：（1）在t-t+△t时间间隔内
△Φt=BLv△t=B?2asin
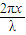?v△t=2Bavsin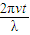△t据法拉第电磁感应定律E=
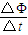得e=2Bavsin
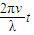
感应电流i=
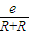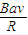=sin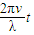可见金属丝上的感应电流是正弦式电流．证毕．
（2）由上知：感应电流的最大值Im=
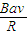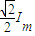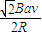
，有效值为I==根据功能关系得：W=Q=I2R总t=
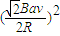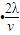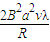
?（2R）=（3）①将两金属丝拉入或拉出磁场区域的过程中，感应电动势最大值为
Em1=2Bav
感应电流最大值 Im1=
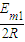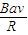
=拉力做功 W1=Q1=
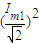
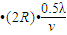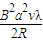
=②拉金属丝穿过磁场区域的过程中，感应电动势最大值为Em2=4Bav
感应电流最大值 Im2=2
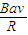
拉力做功 W2=Q2=
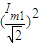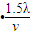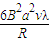
?（2R）=故将两金属丝以速度v匀速拉过磁场外力所做的功为
W′=2W1+W2=2?
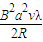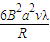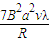
+=答：
（1）证明略．
（2）将两金属丝全部拉入磁场中，外力所做的功为
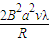．（3）将两金属丝以速度v匀速拉过磁场外力所做的功为
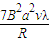．点评：本题关键是运用法拉第定律得到感应电流的表达式，判断出产生了正弦式电流，求电功时应用有效值．
练习册系列答案
相关题目
如图所示，在真空室中平面直角坐标系的y轴竖直向上，x轴上的P点与Q点关于坐标原点O对称，PQ间的距离d=30cm．坐标系所在空间存在一匀强电场，场强的大小E=1.0N/C．一带电油滴在xOy平面内，从P点与x轴成30°的夹角射出，该油滴将做匀速直线运动，已知油滴的速度v=2.0m/s射出，所带电荷量q=1.0×10-7C，重力加速度为g=10m/s2．
（2006?盐城一模）如图所示在xoy所在的平面内，有两根金属丝MN和PQ，其形状分别满足方程y=asin
如图所示，在坐标系xOy所在平面内有一半径为a的圆形区域，圆心坐标O1（a，0），圆内分布有垂直xOy平面的匀强磁场．在坐标原点O处有一个放射源，放射源开口的张角为90°，x轴为它的角平分线．带电粒子可以从放射源开口处在纸面内朝各个方向射出，其速率v、质量m、电荷量+q均相同．其中沿x轴正方向射出的粒子恰好从O1点的正上方的P点射出．不计带电粒子的重力，且不计带电粒子间的相互作用．