题目内容
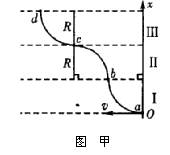
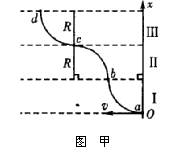
把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物块m与轨道之间的动摩擦因数μ,P点到墙壁的距离为![]() ,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块从静止状态开始释放,那么它第1次撞墙后瞬时速度为零的位置坐标![]() 、第2次撞墙之后速度为零的位置坐标
、第2次撞墙之后速度为零的位置坐标![]() 的表达式分别是什么?
的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度(![]() )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程![]() ?
?

(1)![]() ;
;![]()
(2)它最终会停留在O点;![]()
(3)![]() ;小物块最终人会停留在O点;
;小物块最终人会停留在O点;
解析:
由题意分析知,小物块m沿着轨道滑动时,水平方向上受到二力:
滑动摩擦力![]() 和电场力
和电场力![]()
而且总是有:![]() ①
①
(1)设第一次速度为零的位置坐标为![]() 取墙面为零电势面,则在这一运动过程中应用功能关系有:
取墙面为零电势面,则在这一运动过程中应用功能关系有:
![]() ②
②
![]() ③
③
设第二次速度为零的位置坐标为![]()
取墙面为零电势面,则在第二次运动过程中应用功能关系有:
![]() ④
④
![]()
即:![]() ⑤
⑤
(2)它最终会停留在O点。 ⑥
对从开始到最终的整个运动过程应用功能关系有:
![]() ⑦
⑦
![]() ⑧
⑧
(3)由动量定理知,小物块获得一个向右的初始冲量I,那么向右运动的初速度:
![]() ⑨
⑨
设第一次瞬时速度为零的位置坐标为![]()
取墙面为零电势面,则在这一运动中应用功能关系有:
![]() ⑩
⑩
得: (11)
(11)
即: (12)
(12)
同上道理,对从开始互第一次又回到P点这一过程应用功能关系有:
![]() (13)
(13)
得:![]()
即:![]() (14)
(14)
小物块最终人会停留在O点。 (15)
设从开始到最后一共走的路程为![]() ,全过程应用功能关系有:
,全过程应用功能关系有:
![]() (16)
(16)
得:
即: (17)
(17)

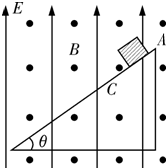 如图所示,在相互垂直的匀强磁场和匀强电场中,有一倾角为θ的足够长的光滑绝缘斜面,磁感应强度为B,方向水平向外,电场强度为E,方向竖直向上.有一质量为m、带电量为+q的小滑块静止在斜面顶端,对斜面的正压力恰好为零.
如图所示,在相互垂直的匀强磁场和匀强电场中,有一倾角为θ的足够长的光滑绝缘斜面,磁感应强度为B,方向水平向外,电场强度为E,方向竖直向上.有一质量为m、带电量为+q的小滑块静止在斜面顶端,对斜面的正压力恰好为零. 如图,在一个分布范围足够大的水平向右的匀强电场中,用长为L的绝缘轻质细丝线把一个带电小球悬挂在O点,小球的质量为m、带电量为q,当小球在A点处于静止状态时,细丝线与竖直方向夹角为θ=30°.现把小球用绝缘工具移动到B位置,使细丝线伸直且水平,无初速释放小球,试求:
如图,在一个分布范围足够大的水平向右的匀强电场中,用长为L的绝缘轻质细丝线把一个带电小球悬挂在O点,小球的质量为m、带电量为q,当小球在A点处于静止状态时,细丝线与竖直方向夹角为θ=30°.现把小球用绝缘工具移动到B位置,使细丝线伸直且水平,无初速释放小球,试求: