题目内容
如图所示，空间有场强E=1.0×102V/m竖直向下的电场，长L=0.8m不可伸长的轻绳固定于O点．另一端系一质量m=0.5kg带电q=5×10－2C的小球。拉起小球至绳水平后在A点无初速度释放，当小球运动至O点的正下方B点时，绳恰好断裂然后垂直打在同一竖直平面且与水平面成θ=53°、无限大的挡板MN上的C点。
试求：
（1）绳子的最大张力；
（2）A、C两点的电势差；
（3）当小球运动C点时，突然施加一恒力F作用在小球上，同时把挡板迅速水平向右移至某处，若小球仍能垂直打在档板上，所加恒力F的方向及取值范围。
（1）
（2）
（3）
【解析】
试题分析：（1）A→B由动能定理及圆周运动知识有：
…………………①
…………………②
联解①②得： …………………③
（2）B→C由功能关系及电场相关知识有：
…………………④
…………………⑤
…………………⑥
联解④⑤⑥得： …………………⑦
（3）由题可知施加恒力F后小球必须做匀速直线或匀加速直线运动，才能垂直打在档板上。
设恒力F与竖直方向的夹角为α，作出小球的受力矢量三角形分析如图所示。（或由矢量三角形可知：当F与F合（或运动）的方向垂直时，F有最小值而无最大值）……⑧
由矢量三角形图有：
…………………⑨
…………………⑩
联解⑨⑩得：
…………………⑾
…………………⑿
考点：考查了粒子在电场中的运动
点评：带电粒子在电场中的运动，综合了静电场和力学的知识，分析方法和力学的分析方法基本相同．先分析受力情况再分析运动状态和运动过程（平衡、加速、减速，直 线或曲线），然后选用恰当的规律解题．解决这类问题的基本方法有两种，第一种利用力和运动的观点，选用牛顿第二定律和运动学公式求解；第二种利用能量转化 的观点，选用动能定理和功能关系求解．
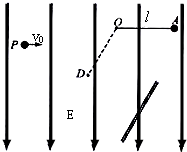（2010?四川）如图所示，空间有场强E=0.5N/C的竖直向下的匀强电场，长l=0.3
如图所示，空间有场强E=1.0×102V/m竖直向下的电场，长L=0.8m不可伸长的轻绳固定于O点．另一端系一质量m=0.5kg带电q=5×10-2C的小球．拉起小球至绳水平后在A点无初速度释放，当小球运动至O点的正下方B点时绳恰好断裂，小球继续运动并垂直打在同一竖直平面且与水平面成θ=53°、无限大的挡板MN上的C点．试求：
如图所示，空间有场强E=1.0×102V/m竖直向下的电场，长l=0.8m不可伸长的轻绳固定于O点．另一端系一质量m=O.5kg带电q=5×10-2C的小球．拉起小球至绳水平后在A点无初速度释放，当小球运动至O点的正下方B点时绳恰好断裂，小球继续运动并垂直打在同一竖直平面且与水平面成θ=53°、无限大的挡板MN上的C点．试求：
如图所示，空间有场强
的竖直向下的匀强电场，长
的不可伸长的轻绳一端固定于
点，另一端系一质量
的不带电小球
，拉起小球至绳水平后，无初速释放。另一电荷量
、质量与
，以速度
水平抛出，经时间
与小球
与
点下方一足够大的平板相遇。不计空气阻力，小球均可视为质点，取
。
到达平板，此时速度恰好为O，求所加的恒力。