题目内容
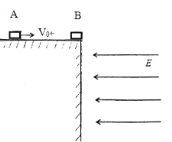
【题目】如图所示，在非常高的光滑、绝缘水平高台边缘，静置一个不带电的小金属块B，另有一与B完全相同的带电量为+q的小金属块A以初速度v0向B运动，A、B的质量均为m。A与B相碰撞后，两物块立即粘在一起，并从台上飞出。已知在高台边缘的右面空间中存在水平向左的匀强电场，场强大小E=2mg/q。求：
（1）A、B一起运动过程中距高台边缘的最大水平距离
（2）A、B运动过程的最小速度为多大
（3）从开始到A、B运动到距高台边缘最大水平距离的过程 A损失的机械能为多大？
【答案】（1）由动量守恒定律：mυ0=2mυ……2分
碰后水平方向：qE=2ma
…2分
-2aXm=0-υ2…2分
得：
……1分
（2）在t时刻，A、B的水平方向的速度为
…………………1分
竖直方向的速度为υγ=gt………………………………………………1分
合速度为：
……………………………………………2分
解得υ合的最小值：
……………………………………3分
（3）碰撞过程中A损失的机械能：
………2分
碰后到距高台边缘最大水平距离的过程中A损失的机械能：
…………………………………………………………2分
从开始到A、B运动到距离高台边缘最大水平距离的过程中A损失的机械能为：
……………………………………………………………2分
【解析】
由动量守恒定律列出等式，根据运动学公式求出距高台边缘的最大水平距离；根据运动学公式求出A、B运动过程的最小速度；根据能量守恒定律求出损失的机械能；
解：(1)由动量守恒定律：
①
碰后水平方向：
②
又：③
设水平方向运动距离
得：
④
由①②③④解得：
⑤
(2)在t时刻，A、B的水平方向的速度为：
⑥
在t时刻，A、B竖直方向的速度为：
⑦
合速度为：
⑧
由⑥⑦⑧解得
的最小值：
(3)碰撞过程中A损失的机械能：
⑨
碰后到距高台边缘最大水平距离的过程中A损失的机械能：
⑩
由⑨⑩可知，从开始到A、B运动到距离高台边缘最大水平距离的过程中A损失的机械能为：
名校课堂系列答案
