题目内容
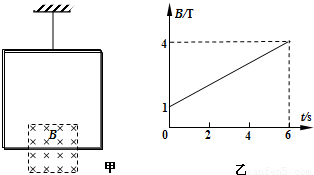
轻质细线吊着一质量为m=0.32kg,边长为L=0.8m、匝数n=10的正方形线圈总电阻为r=1Ω.边长为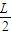 的正方形磁场区域对称分布在线圈下边的两侧,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经t时间细线开始松驰,g=10m/s2.求:
的正方形磁场区域对称分布在线圈下边的两侧,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经t时间细线开始松驰,g=10m/s2.求:(1)在前t时间内线圈中产生的电动势;
(2)在前t时间内线圈的电功率;
(3)求t的值.
【答案】分析:(1)根据?=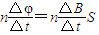 求出感应电动势,注意S为有效面积.
求出感应电动势,注意S为有效面积.
(2)根据感应电动势求出感应电流,再根据P=I2r求出线圈的电功率.
(3)当线圈所受的安培力等于线圈的重力时,绳子的张力为零,细线开始松弛.根据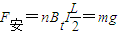 ,
,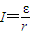 求出拉力为零时的磁感应强度,再根据图象求出时间.
求出拉力为零时的磁感应强度,再根据图象求出时间.
解答:解:(1)由法拉第电磁感应定律得: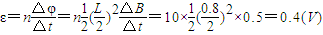
故在前t时间内线圈中产生的电动势为0.4V.
(2)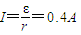
P=I2r=0.16(W)
故在前t时间内线圈的电功率为0.16W.
(3)分析线圈受力可知,当细线松弛时有: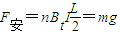
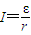
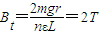
由图象知: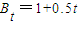 解得:t=2s
解得:t=2s
故t的值为2s.
点评:解决本题的关键掌握法拉第电磁感应定律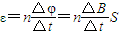 .以及知道细线开始松驰时,线圈所受的安培力和重力平衡.
.以及知道细线开始松驰时,线圈所受的安培力和重力平衡.
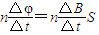 求出感应电动势,注意S为有效面积.
求出感应电动势,注意S为有效面积.(2)根据感应电动势求出感应电流,再根据P=I2r求出线圈的电功率.
(3)当线圈所受的安培力等于线圈的重力时,绳子的张力为零,细线开始松弛.根据
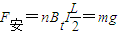 ,
,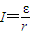 求出拉力为零时的磁感应强度,再根据图象求出时间.
求出拉力为零时的磁感应强度,再根据图象求出时间.解答:解:(1)由法拉第电磁感应定律得:
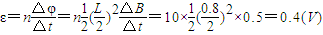
故在前t时间内线圈中产生的电动势为0.4V.
(2)
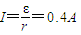
P=I2r=0.16(W)
故在前t时间内线圈的电功率为0.16W.
(3)分析线圈受力可知,当细线松弛时有:
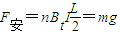
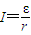
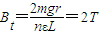
由图象知:
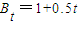 解得:t=2s
解得:t=2s故t的值为2s.
点评:解决本题的关键掌握法拉第电磁感应定律
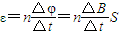 .以及知道细线开始松驰时,线圈所受的安培力和重力平衡.
.以及知道细线开始松驰时,线圈所受的安培力和重力平衡. 
练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 (2011?深圳一模)轻质细线吊着一质量为m=0.32kg,边长为L=0.8m、匝数n=10的正方形线圈总电阻为r=1Ω.边长为
(2011?深圳一模)轻质细线吊着一质量为m=0.32kg,边长为L=0.8m、匝数n=10的正方形线圈总电阻为r=1Ω.边长为 (2011?昌平区二模)轻质细线吊着一质量为m=0.64kg、边长为L=0.8m、匝数n=10的正方形线圈abcd,线圈总电阻为R=1Ω.边长为L/2正方形磁场区域对称分布在线圈下边的两侧,如图(甲)所示.磁场方向垂直纸面向里,磁感应强度大小随时间变化如图(乙)所示,从t=0开始经t0时间细线开始松驰,取g=10m/s2.求:
(2011?昌平区二模)轻质细线吊着一质量为m=0.64kg、边长为L=0.8m、匝数n=10的正方形线圈abcd,线圈总电阻为R=1Ω.边长为L/2正方形磁场区域对称分布在线圈下边的两侧,如图(甲)所示.磁场方向垂直纸面向里,磁感应强度大小随时间变化如图(乙)所示,从t=0开始经t0时间细线开始松驰,取g=10m/s2.求:
 ,边长为
,边长为 的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
 ,边长为
,边长为 的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求:
的正方形磁场区域对称分布在线图下边的两侧,如图甲所示,磁场方向垂直纸面向里,大小随时间变化如图乙所示,从t=0开始经时间t0细线开始松驰,g=10m/s2。求: