题目内容
17.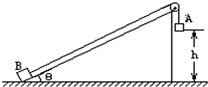 如图所示,用细绳连接的A、B两物体质量均为m,B位于倾角为30°的足够长的光滑斜面上,细绳跨过定滑轮后使A、B均保持静止,然后释放,A下降1m后落地,不计滑轮质量与摩擦,求:
如图所示,用细绳连接的A、B两物体质量均为m,B位于倾角为30°的足够长的光滑斜面上,细绳跨过定滑轮后使A、B均保持静止,然后释放,A下降1m后落地,不计滑轮质量与摩擦,求:(1)A下落过程中绳子的拉力;
(2)物块B沿斜面上升的最大距离s?
分析 (1)采用隔离法,分别对A和B,运用牛顿第二定律列式,即可求得绳子的拉力.
(2)由运动学公式求出A落地时的速度.A落地后B继续沿斜面上升,再由机械能守恒求B继续上升的距离,从而得到最大距离s.
解答 解:(1)A下落过程中,根据牛顿第二定律得:
对A:mg-T=ma
对B:T-mgsin30°=ma
联立解得 a=0.5g,T=0.5mg
(2)A落地时的速度 v=$\sqrt{2ah}$=$\sqrt{2×0.5×10×1}$=$\sqrt{10}$m/s
A落地后B继续沿斜面上升,设B继续上升的距离为l,由机械能守恒得:
mglsin30°=$\frac{1}{2}m{v}^{2}$
解得 l=1m
故B沿斜面上升的最大距离 s=h+l=2m
答:
(1)A下落过程中绳子的拉力是0.5mg;
(2)物块B沿斜面上升的最大距离s是2m.
点评 A下落过程中,两个物体的加速度不同,最好用隔离法求拉力和加速度.对于B继续上升的过程,要根据机械能守恒的条件判断出其机械能是守恒的,当然也可以根据动能定理求上滑的距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 放在光滑水平桌面上的A、B木块中间夹一被压缩的弹簧,当弹簧放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上,A的落地点与桌边的水平距离为0.5m,B的落地点与桌边的水平距离为1m,那么( )
放在光滑水平桌面上的A、B木块中间夹一被压缩的弹簧,当弹簧放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上,A的落地点与桌边的水平距离为0.5m,B的落地点与桌边的水平距离为1m,那么( )
 放在光滑水平桌面上的A、B木块中间夹一被压缩的弹簧,当弹簧放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上,A的落地点与桌边的水平距离为0.5m,B的落地点与桌边的水平距离为1m,那么( )
放在光滑水平桌面上的A、B木块中间夹一被压缩的弹簧,当弹簧放开时,它们各自在桌面上滑行一段距离后,飞离桌面落在地上,A的落地点与桌边的水平距离为0.5m,B的落地点与桌边的水平距离为1m,那么( )| A. | A、B离开弹簧时的速度比为2:1 | |
| B. | A、B质量比为2:1 | |
| C. | 未离开弹簧时,A、B所受冲量比为1:2 | |
| D. | 未离开弹簧时,A、B加速度之比为1:2 |
8.下列元件利用温度传感器的是( )
| A. | 火灾报警器 | B. | 电熨斗 | C. | 电饭锅 | D. | 电子秤 |
12.一个质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面.已知该物体做匀减速运动的加速度为$\frac{3}{4}$g,在斜面上上升的最大高度为h,则此过程中( )
| A. | 物体的动能减少了mgh | B. | 物体克服重力做功mgh | ||
| C. | 物体的机械能守恒 | D. | 物体克服摩擦力做功$\frac{mgh}{2}$ |
9.根据牛顿第一定律,下列说法中正确的是( )
| A. | 静止的物体一定不受其他物体的作用 | |
| B. | 物体受力才会运动,当外力停止作用后,物体会慢慢停下来 | |
| C. | 物体运动状态发生变化,物体一定受到外力作用 | |
| D. | 物体不受力的作用,运动状态也能改变 |
3.关于运动的合成与分解,下列说法正确的是( )
| A. | 合运动的速度一定大于两个分运动的速度 | |
| B. | 合运动的时间一定大于分运动的时间 | |
| C. | 两个直线运动的合运动一定是直线运动 | |
| D. | 两个匀速直线运动的合运动一定是直线运动 |
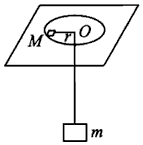 如图,细绳一端系着质量M=0.6㎏的物体,静止在水平面,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(取g=9.8m/s2)
如图,细绳一端系着质量M=0.6㎏的物体,静止在水平面,另一端通过光滑小孔吊着质量m=0.3kg的物体,M的中点与圆孔距离为0.2m,并知M和水平面的最大静摩擦力为2N,现使此平面绕中心轴线转动,问角速度ω在什么范围m会处于静止状态?(取g=9.8m/s2)
