题目内容
如图,一倾角为30°的光滑斜面,底端有一与斜面垂直的固定档板M,物块A、B之间用一与斜面平行轻质弹簧连结,现用力缓慢沿斜面向下推动物块B,当弹簧具有5J弹性势能时撤去推力,释放物块B;已知A、B质量分别为5kg、2kg,弹簧的弹性势能表达式为EP= ,其中k为弹簧的劲度系数,大小为1000N/m,x为弹簧形变量.(g取10m/s2)
,其中k为弹簧的劲度系数,大小为1000N/m,x为弹簧形变量.(g取10m/s2)(1)求当弹簧恢复原长时,物块B的速度;
(2)试判断在B上升过程中,能否将A 拉离档板?若能,请计算A刚离开档板时B的动能;若不能,请计算B在最高点处的加速度.

【答案】分析:(1)弹簧减小的弹性势能等于物块B增加的机械能,根据守恒定律列式求解;
(2)物块A刚离开挡板时,受重力、斜面支持力和弹簧的拉力,根据平衡条件求解出拉力;根据胡克定律求解弹簧的伸长量,最后根据减小的弹性势能等于物块B增加的机械能列式求解.
解答:解:(1)由 得,刚撤去推力时,弹簧的压缩量x1=0.1m…①
得,刚撤去推力时,弹簧的压缩量x1=0.1m…①
弹簧恢复原长的过程中,物块B和弹簧组成的系统机械能守恒,
由 …②得
…②得
v=2m/s…③
(2)假设A能被拉离挡板,在A刚被拉离时,有弹簧弹力F=mAgsinθ…④
结合F=kx2,此时弹簧伸长量x2=0.025m…⑤
此时弹性势能EP=0.3125J…⑥
相对于弹簧原长处重力势能增量为△EP=mBg△h=0.25J…⑦
因为弹簧处于原长时物块B的动能 J…⑧
J…⑧
由于Ek0>EP+△EP,所以能将物块A 拉离档板,且此时物块B的动能为:Ekt=Ek0-EP-△EP,得Ekt=3.44J…⑨
答:
(1)当弹簧恢复原长时,物块B的速度为2m/s;
(2)在B上升过程中,能将物块A拉离档板,且此时物块B的动能为3.44J.
点评:本题关键明确系统机械能守恒,要考虑弹性势能、重力势能、动能三种能量的转化,不难.
(2)物块A刚离开挡板时,受重力、斜面支持力和弹簧的拉力,根据平衡条件求解出拉力;根据胡克定律求解弹簧的伸长量,最后根据减小的弹性势能等于物块B增加的机械能列式求解.
解答:解:(1)由
 得,刚撤去推力时,弹簧的压缩量x1=0.1m…①
得,刚撤去推力时,弹簧的压缩量x1=0.1m…①弹簧恢复原长的过程中,物块B和弹簧组成的系统机械能守恒,
由
 …②得
…②得v=2m/s…③
(2)假设A能被拉离挡板,在A刚被拉离时,有弹簧弹力F=mAgsinθ…④
结合F=kx2,此时弹簧伸长量x2=0.025m…⑤
此时弹性势能EP=0.3125J…⑥
相对于弹簧原长处重力势能增量为△EP=mBg△h=0.25J…⑦
因为弹簧处于原长时物块B的动能
 J…⑧
J…⑧由于Ek0>EP+△EP,所以能将物块A 拉离档板,且此时物块B的动能为:Ekt=Ek0-EP-△EP,得Ekt=3.44J…⑨
答:
(1)当弹簧恢复原长时,物块B的速度为2m/s;
(2)在B上升过程中,能将物块A拉离档板,且此时物块B的动能为3.44J.
点评:本题关键明确系统机械能守恒,要考虑弹性势能、重力势能、动能三种能量的转化,不难.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
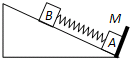 如图,一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上.现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B.已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为
如图,一倾角为θ=30°的足够长固定光滑斜面底端有一与斜面垂直的挡板M,物块A、B之间用一与斜面平行的轻质弹簧连接且静止在斜面上.现用外力沿斜面向下缓慢推动物块B,当弹簧具有5J的弹性势能时撤去推力,释放物块B.已知物块A、B的质量分别为5kg和10kg,弹簧的弹性势能的表达式为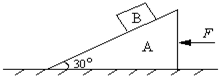 如图,一倾角为30°的直角三角形物块A,质量为m1,在其斜面上放置一质量为m2的物块B,物块与斜面间无摩擦,为了使B相对斜面静止,需A在水平面上向左作匀加速运动.
如图,一倾角为30°的直角三角形物块A,质量为m1,在其斜面上放置一质量为m2的物块B,物块与斜面间无摩擦,为了使B相对斜面静止,需A在水平面上向左作匀加速运动.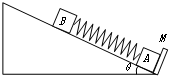 如图,一倾角为30°的光滑斜面,底端有一与斜面垂直的固定档板M,物块A、B之间用一与斜面平行轻质弹簧连结,现用力缓慢沿斜面向下推动物块B,当弹簧具有5J弹性势能时撤去推力,释放物块B;已知A、B质量分别为5kg、2kg,弹簧的弹性势能表达式为EP=
如图,一倾角为30°的光滑斜面,底端有一与斜面垂直的固定档板M,物块A、B之间用一与斜面平行轻质弹簧连结,现用力缓慢沿斜面向下推动物块B,当弹簧具有5J弹性势能时撤去推力,释放物块B;已知A、B质量分别为5kg、2kg,弹簧的弹性势能表达式为EP=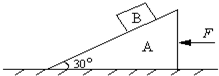 如图,一倾角为30°的直角三角形物块A,质量为m1,在其斜面上放置一质量为m2的物块B,物块与斜面间无摩擦,为了使B相对斜面静止,需A在水平面上向左作匀加速运动.
如图,一倾角为30°的直角三角形物块A,质量为m1,在其斜面上放置一质量为m2的物块B,物块与斜面间无摩擦,为了使B相对斜面静止,需A在水平面上向左作匀加速运动.