题目内容
 如图,倾角为θ的斜面固定.有n个质量都为m的相同的小木块(可视为质点)放置在斜面上.相邻两小木块间距离都为l,最下端的木块距底端也是l,小木块与斜面间的动摩擦因数都为μ.在开始时刻,第一个小木块从斜面顶端以初速度v0沿斜面下滑,其余所有木块都静止,由于第一个木块的下滑将依次引起一系列的碰撞.设每次碰撞的时间极短,在每次碰撞后,发生碰撞的木块都粘在一起运动,直到最后第n个木块到达底端时,速度刚好为零.已知重力加速度为g.求:
如图,倾角为θ的斜面固定.有n个质量都为m的相同的小木块(可视为质点)放置在斜面上.相邻两小木块间距离都为l,最下端的木块距底端也是l,小木块与斜面间的动摩擦因数都为μ.在开始时刻,第一个小木块从斜面顶端以初速度v0沿斜面下滑,其余所有木块都静止,由于第一个木块的下滑将依次引起一系列的碰撞.设每次碰撞的时间极短,在每次碰撞后,发生碰撞的木块都粘在一起运动,直到最后第n个木块到达底端时,速度刚好为零.已知重力加速度为g.求:(1)第一次碰撞后小木块1的速度大小v;
(2)从第一个小木块开始运动到第一次碰撞后系统损失的机械能△E;
(3)发生一系列碰撞后,直到最后第n个木块到达底端,在整个过程中,由于碰撞所损失的总机械能△E总.
分析:(1)由动能定理可求出小木块1碰前的速度,再由动量守恒可求出小木块1碰撞后的速度大小;
(2)碰撞前因摩擦力做功,导致小木块机械能损失;再求出碰撞后小木块动能的减小导致机械能损失;从而两者之和即为从第一个小木块开始运动到第一次碰撞后系统损失的机械能;
(3)通过力做功表达式求出碰撞整个过程中,重力、摩擦力做功;再根据功能关系可求出在碰撞中总机械能损失.
(2)碰撞前因摩擦力做功,导致小木块机械能损失;再求出碰撞后小木块动能的减小导致机械能损失;从而两者之和即为从第一个小木块开始运动到第一次碰撞后系统损失的机械能;
(3)通过力做功表达式求出碰撞整个过程中,重力、摩擦力做功;再根据功能关系可求出在碰撞中总机械能损失.
解答:解:(1)设小木块1碰前的速度为v1,从开始运动到碰前,
根据动能定理:mglsinθ-μmglcosθ=
m
-
m
对小木块1和2,由动量守恒 mv1=2mv
则有 v=
(2)碰撞前损失的机械能为△E1=μmglcosθ
因碰撞损失的机械能为 △E2=
m
-
?2mv2
则有△E=△E1+△E2=
m
+
mgl(sinθ-μcosθ)
(3)对n个木块碰撞的全过程
重力做的总功 WG=mglsinθ(1+2+3+…+n)=
mglsinθ
克服摩擦做的总功
Wf=μmglcosθ(1+2+3+…+n)=
μmglcosθ
根据功与能的关系 WG+
m
=Wf+△E总
由以上各式求出 △E总=
m
+
mgl(sinθ-μcosθ)
答:(1)第一次碰撞后小木块1的速度大小 v=
;
(2)从第一个小木块开始运动到第一次碰撞后系统损失的机械能△E=△E1+△E2=
m
+
mgl(sinθ-μcosθ);
(3)发生一系列碰撞后,直到最后第n个木块到达底端,在整个过程中,由于碰撞所损失的总机械能 △E总=
m
+
mgl(sinθ-μcosθ).
根据动能定理:mglsinθ-μmglcosθ=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
对小木块1和2,由动量守恒 mv1=2mv
则有 v=
| 1 |
| 2 |
|
(2)碰撞前损失的机械能为△E1=μmglcosθ
因碰撞损失的机械能为 △E2=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
则有△E=△E1+△E2=
| 1 |
| 4 |
| v | 2 0 |
| 1 |
| 2 |
(3)对n个木块碰撞的全过程
重力做的总功 WG=mglsinθ(1+2+3+…+n)=
| n(n+1) |
| 2 |
克服摩擦做的总功
Wf=μmglcosθ(1+2+3+…+n)=
| n(n+1) |
| 2 |
根据功与能的关系 WG+
| 1 |
| 2 |
| v | 2 0 |
由以上各式求出 △E总=
| 1 |
| 2 |
| v | 2 0 |
| n(n+1) |
| 2 |
答:(1)第一次碰撞后小木块1的速度大小 v=
| 1 |
| 2 |
|
(2)从第一个小木块开始运动到第一次碰撞后系统损失的机械能△E=△E1+△E2=
| 1 |
| 4 |
| v | 2 0 |
| 1 |
| 2 |
(3)发生一系列碰撞后,直到最后第n个木块到达底端,在整个过程中,由于碰撞所损失的总机械能 △E总=
| 1 |
| 2 |
| v | 2 0 |
| n(n+1) |
| 2 |
点评:本题是力学综合题,考查动能定理、动量守恒定律、功的公式、功与能关系等规律,同时动量守恒定律注意矢量性及功的正负.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,倾角为30°的斜面上放一有支架的小车,支架末端用细线挂一小球.拉着小车沿斜面下滑时,小球与小车相对静止.重力加速度为g,求下述三种情况下小车的加速度.
如图,倾角为30°的斜面上放一有支架的小车,支架末端用细线挂一小球.拉着小车沿斜面下滑时,小球与小车相对静止.重力加速度为g,求下述三种情况下小车的加速度. 如图,倾角为37°的斜面上一重力为50N的木块恰好匀速下滑,sin37°=0.6,求
如图,倾角为37°的斜面上一重力为50N的木块恰好匀速下滑,sin37°=0.6,求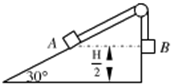 如图,倾角为300的斜面高为H,顶端有一小滑轮,物块A和B的质量分别为m1和m2,通过轻绳连接,不计一切摩擦.开始时两物块都位于离地面高为H/2的位置,由静止释放两物块后,若物块A恰好能到达斜面顶端,求:
如图,倾角为300的斜面高为H,顶端有一小滑轮,物块A和B的质量分别为m1和m2,通过轻绳连接,不计一切摩擦.开始时两物块都位于离地面高为H/2的位置,由静止释放两物块后,若物块A恰好能到达斜面顶端,求: 如图,倾角为15°的斜面上放着一个木箱,100N的拉力F斜向上拉着木箱,F与水平方向成45°角.分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立坐标系,把F分解为沿着两个坐标轴的分力.试在图中作出Fx和Fy,并计算两个分力大小.
如图,倾角为15°的斜面上放着一个木箱,100N的拉力F斜向上拉着木箱,F与水平方向成45°角.分别以平行于斜面和垂直于斜面的方向为x轴和y轴建立坐标系,把F分解为沿着两个坐标轴的分力.试在图中作出Fx和Fy,并计算两个分力大小.