题目内容
12.河宽L=300m,河水流速v1=3m/s,船在静水中的速度v2=5m/s.欲按下列要求过河时,过河时间为多少?(1)以最短的时间过河;
(2)以最小的位移过河.
分析 (1)当船头方向与河岸方向垂直时,渡河时间最短,抓住等时性,结合垂直河岸方向的速度和位移求出渡河的时间.
(2)当合速度方向与河岸垂直时,渡河位移最短,根据平行四边形定则求出船头的方向,根据河宽和合速度的大小求出渡河的时间.
解答  解:(1)当船头与河岸方向垂直时,过河的时间最短,过河时间为:
解:(1)当船头与河岸方向垂直时,过河的时间最短,过河时间为:
t=$\frac{L}{{v}_{2}}$=$\frac{300}{5}$s=60s,
(2)因v2>v1,所以应使船的合速度方向垂直于河岸,令此时船头与河岸方向的夹角为α,如图所示,
船过河的最小位移,即为河宽,为300m,
那么合速度为v=$\sqrt{{v}_{2}^{2}-{v}_{1}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4m/s;
因此以最小位移过河的时间为t′=$\frac{300}{4}$=75s;
答:(1)以最短的时间过河的时间为60s;
(2)以最小的位移过河时间为75s.
点评 本题考查了小船渡河问题,知道当船头的方向与河岸垂直时,渡河时间最短,当合速度方向与河岸垂直时,渡河位移最短.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
3.对于做斜上抛运动的物体,下列说法中正确的是(不计空气阻力)( )
| A. | 抛射角一定时,初速度越大,飞行时间越长 | |
| B. | 初速度一定时,抛射角越大,射高越小 | |
| C. | 初速度一定时,抛射角越大,射程一定越大 | |
| D. | 到达最高点时,物体速度为零,加速度不为零 |
20. 如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )
如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )
 如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )
如图,为汽车在水平路面上启动过程的v-t图象.0~t1时间内为匀加速阶段,t1~t2时间内表示以额定功率行驶时的变加速阶段,t2后是与t轴平行的直线,设整个过程中汽车所受阻力恒定,则下列说法正确的是( )| A. | 0~t1时间内,牵引力增大,功率不变 | |
| B. | 0~t1时间内,牵引力为阻力的$\frac{{v}_{2}}{{v}_{1}}$倍 | |
| C. | 若v2=2v1,则0~t1时间内,牵引力做的功为mv12 | |
| D. | 若t2=2t1,则t1~t2时间内,牵引力做的功为mv22($\frac{{v}_{2}}{{v}_{2}-{v}_{1}}$) |
7.以下说法正确的是( )
| A. | 对不同星球的行星或卫星,公式$\frac{{R}^{3}}{{T}^{2}}$=K中的K值不相同 | |
| B. | 开普勒关于行星的运动公式$\frac{{R}^{3}}{{T}^{2}}$=K中的K是于行星无关的常量 | |
| C. | 天王星是人们依据万有引力定律计算出它的轨道而发现的 | |
| D. | 万有引力常量G是牛顿通过实验测出的,并应用了科学放大思想 |
4.质量为M的原子核,原来处于静止状态,当它以速度v放出一个质量为m的粒子时,剩余部分的速度为( )
| A. | $\frac{mv}{M-m}$ | B. | -$\frac{mv}{M+m}$ | C. | $\frac{mv}{M+m}$ | D. | -$\frac{mv}{M-m}$ |
2. 如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
 如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )
如图,一只蚂蚁从A点出发,沿边长为a的正方形路线爬行,经过B、C、D后又回到A点,则在这一过程中( )| A. | 蚂蚁的位移大小为4a | B. | 蚂蚁的位移为零 | ||
| C. | 蚂蚁运动的路程为零 | D. | 蚂蚁运动的路程和位移都为零 |
 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.若用一张印有小方格的纸记录轨迹,小方格的边长为5cm,小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的大小为v0=1.4m/s(g取9.8m/s2).
在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.若用一张印有小方格的纸记录轨迹,小方格的边长为5cm,小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的大小为v0=1.4m/s(g取9.8m/s2).
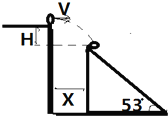 如图所示,一小球自平台上水平抛出,恰好落在平台前一倾角α=53°的斜面顶端,并刚好沿斜面下滑(此时速度方向沿斜面方向),已知斜面顶端与平台高度差h=0.8m,g=10m/s2,则小球水平抛出的初速度为3m/s,斜面与平台边缘的水平距离为1.2m.
如图所示,一小球自平台上水平抛出,恰好落在平台前一倾角α=53°的斜面顶端,并刚好沿斜面下滑(此时速度方向沿斜面方向),已知斜面顶端与平台高度差h=0.8m,g=10m/s2,则小球水平抛出的初速度为3m/s,斜面与平台边缘的水平距离为1.2m.