题目内容
14. 如图所示,质量为M的小车静止在光滑的水平地面上,其AB部分为半径R=0.6m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=2m,一可看做质点质量为m的小物块从A点由静止释放,滑到C点刚好相对小车静止.已知小物块质量M=3m,g取10m/s2,求:
如图所示,质量为M的小车静止在光滑的水平地面上,其AB部分为半径R=0.6m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=2m,一可看做质点质量为m的小物块从A点由静止释放,滑到C点刚好相对小车静止.已知小物块质量M=3m,g取10m/s2,求:(1)小物块与小车BC部分间的动摩擦因数;
(2)小物块从A滑到C的过程中,小物块获得的最大速度.
分析 (1)根据动量守恒定律可明确共速时静止,根据功能关系即可求得动摩擦因数;
(2)滑块滑到B点时,小车速度最大;当滑块滑到C点时,小车和滑块相对静止,根据动量守恒定律和功能关系列式求解即可.
解答 解:(1)m滑至C,设系统的速度为v.根据动量守恒定律得 (m+M)v=0,得 v=0,所以最终系统静止
根据功能关系,有:
mgR=μmgL
解得:μ=$\frac{R}{L}$=$\frac{0.6}{2}$=0.3
(2)
滑至B时,车速最大,规定向右为正方向,物块与车组成的系统水平方向动量守恒,有:
mvm-MvM=0
由动能关系:mgR=$\frac{1}{2}$mvm2+$\frac{1}{2}$MVM2
联立解得:vM=1.0m/s
方向水平向左.
答:(1)小物块与小车BC部分间的动摩擦因数为0.3;
(2)小物块从A滑到C的过程中,小车获得的最大速度1.0m/s.
点评 本题关键分析清楚系统的运动情况,知道系统水平方向动量守恒,竖直方向动量不守恒,同时根据功能关系列式求解.

练习册系列答案
相关题目
5.对做曲线运动的物体,下列说法正确的是( )
| A. | 物体的加速度一定是变化的 | B. | 物体的速度大小一定是变化的 | ||
| C. | 物体的速度方向一定是变化的 | D. | 物体所受的合外力可能为零 |
2. 人们发现,不同的原子核,其核子的平均质量(原子核的质量除以核子数)与原子序数有如图所示的关系.下列关于原子结构和核反应的说法正确的是( )
人们发现,不同的原子核,其核子的平均质量(原子核的质量除以核子数)与原子序数有如图所示的关系.下列关于原子结构和核反应的说法正确的是( )
 人们发现,不同的原子核,其核子的平均质量(原子核的质量除以核子数)与原子序数有如图所示的关系.下列关于原子结构和核反应的说法正确的是( )
人们发现,不同的原子核,其核子的平均质量(原子核的质量除以核子数)与原子序数有如图所示的关系.下列关于原子结构和核反应的说法正确的是( )| A. | 由图可知,原子核A裂变成原子核B和C时会有质量亏损,要放出能量 | |
| B. | 由图可知,原子核A裂变成原子核B和C时会有质量亏损,要吸收能量 | |
| C. | 由图可知,原子核D和E聚变成原子核F时会有质量亏损,要吸收能量 | |
| D. | 由图可知,原子核D和E聚变成原子核F时会有质量亏损,要放出能量 |
9.下列物理量中,属于矢量的是( )
| A. | 动量 | B. | 动能 | C. | 功 | D. | 功率 |
10. 中国第一颗人造地球卫星绕地球沿椭圆轨道运动,地球位于椭圆的一个焦点上,如图,卫星从A点运动到远地点B的过程中( )
中国第一颗人造地球卫星绕地球沿椭圆轨道运动,地球位于椭圆的一个焦点上,如图,卫星从A点运动到远地点B的过程中( )
 中国第一颗人造地球卫星绕地球沿椭圆轨道运动,地球位于椭圆的一个焦点上,如图,卫星从A点运动到远地点B的过程中( )
中国第一颗人造地球卫星绕地球沿椭圆轨道运动,地球位于椭圆的一个焦点上,如图,卫星从A点运动到远地点B的过程中( )| A. | 地球对卫星的引力越来越小 | B. | 地球对卫星的引力越来越大 | ||
| C. | 卫星的运行速度越来越小 | D. | 卫星的运行速度越来越大 |
7.有关光的本性,下列说法中正确的是( )
| A. | 光具有波动性,又具有粒子性,这是相互矛盾和对立的 | |
| B. | 光的干涉,衍射现象证明光具有粒子性,光电效应现象证明光具有波动性 | |
| C. | 大量光子才具有波动性,个别光子只具有粒子性 | |
| D. | 由于光既具有波动性,又具有粒子性,无法只用其中一种去说明光的一切现象,只能认为光具有波粒二象性 |
8. 如图所示,一物体受斜向上的拉力F作用静止在水平地面上,现增大拉力F的大小,物体仍静止,下列说法正确的是( )
如图所示,一物体受斜向上的拉力F作用静止在水平地面上,现增大拉力F的大小,物体仍静止,下列说法正确的是( )
 如图所示,一物体受斜向上的拉力F作用静止在水平地面上,现增大拉力F的大小,物体仍静止,下列说法正确的是( )
如图所示,一物体受斜向上的拉力F作用静止在水平地面上,现增大拉力F的大小,物体仍静止,下列说法正确的是( )| A. | 物体受到的合力变大 | B. | 物体可能受三个力作用 | ||
| C. | 地面受到的压力变小 | D. | 物体受到的摩擦力变大 |
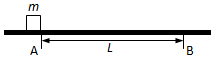 如图,质量m=2kg的物体静止于水平地面上的A处,已知A、B间距L=20m,物体与地面间的动摩擦因数μ=0.5.
如图,质量m=2kg的物体静止于水平地面上的A处,已知A、B间距L=20m,物体与地面间的动摩擦因数μ=0.5.