题目内容
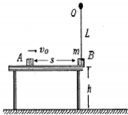 如图所示,水平桌面的右端有一质量为m的物块B,用长为L=0.3m的不可伸长的细线悬挂,B对水平桌面压力刚好为零,水平桌面离地面的高度为h=5.0m,另一质量为2m的物块A在距水平桌面的右端s=4.0m处以vo=5.0m/s的水平初速度向右运动,并与B发生碰撞,已知A与桌面间的动摩擦因数为μ=0.2,碰后A速度为1.0m/s,物块均可视为质点,取g=l 0m/s2.
如图所示,水平桌面的右端有一质量为m的物块B,用长为L=0.3m的不可伸长的细线悬挂,B对水平桌面压力刚好为零,水平桌面离地面的高度为h=5.0m,另一质量为2m的物块A在距水平桌面的右端s=4.0m处以vo=5.0m/s的水平初速度向右运动,并与B发生碰撞,已知A与桌面间的动摩擦因数为μ=0.2,碰后A速度为1.0m/s,物块均可视为质点,取g=l 0m/s2.(1)求 A与B碰撞前的速度大小;
(2)求碰撞后A的落地点与桌面右端的水平距离x;
(3)通过计算判断A与B碰后,物块B能否绕0点在竖直平面内做完整的圆周运动.
分析:(1)从A运动到B,只有摩擦力做功,根据动能定理求出A与B碰撞前的速度大小.
(2)A、B发生弹性碰撞,根据动量守恒定律和能量守恒定律分别求出A、B碰撞前后的速度,根据高度求出平抛运动的时间,再根据A的速度和时间求出水平距离.
(3)物块A与物块B碰后,若物块能够做圆周运动,最高点的拉力恰好为零.根据动能定理求出物块在最高点的速度,进而判断.
(2)A、B发生弹性碰撞,根据动量守恒定律和能量守恒定律分别求出A、B碰撞前后的速度,根据高度求出平抛运动的时间,再根据A的速度和时间求出水平距离.
(3)物块A与物块B碰后,若物块能够做圆周运动,最高点的拉力恰好为零.根据动能定理求出物块在最高点的速度,进而判断.
解答:解:(1)设碰撞前A的速度为v,由动能定理-μ?2mgs=
×2mv2-
×2m
解得:v=
=3.0m/s
(2)设碰撞后A速度为vA、,且设向右为正方向;
x=vAt,h=
gt2
解得:x=1.0m
(3)设碰后B的速度为vB,根据动量守恒定律,得:
2mv=2mvA+mvB
解得:
=4m/s
若物块B在碰后做完整的圆周运动,到达最高点的速度:
由机械能守恒定律得:
m
=
m
+mg?2L
解得:
=2m/s
物块B恰好能过最高点时:mg=
解得:v最=
m/s<
所以物块B能在竖直平面内做完整的圆周运动.
答:(1)A与B碰撞前的速度大小是3m/s;
(2)碰撞后A的落地点与桌面右端的水平距离是1.0m;
(3)物块B能在竖直平面内做完整的圆周运动.
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得:v=
|
(2)设碰撞后A速度为vA、,且设向右为正方向;
x=vAt,h=
| 1 |
| 2 |
解得:x=1.0m
(3)设碰后B的速度为vB,根据动量守恒定律,得:
2mv=2mvA+mvB
解得:
| v | ′ B |
若物块B在碰后做完整的圆周运动,到达最高点的速度:
| v | ′ B |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | ′2 B |
解得:
| v | ′ B |
物块B恰好能过最高点时:mg=
m
| ||
| L |
解得:v最=
| 3 |
| v | ′ B |
所以物块B能在竖直平面内做完整的圆周运动.
答:(1)A与B碰撞前的速度大小是3m/s;
(2)碰撞后A的落地点与桌面右端的水平距离是1.0m;
(3)物块B能在竖直平面内做完整的圆周运动.
点评:本题综合运用了动能定理、动量守恒定律和牛顿运动定律,第(3)问,要判断是否恰好能做圆周运动.

练习册系列答案
相关题目
 如图所示,水平放置的轻弹簧左端固定,小物块P置于光滑水平桌面上的A点并与弹簧的右端接触且不粘连,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=8J.撤去推力后,P沿桌面滑到停在光滑水平面的平板小车Q上,小车的上表面与桌面在同一水平面上.已知P、Q质量分别为m=1Kg、M=4Kg,P与Q的动摩擦因数为μ=0.4.取g=10m/s2,求:
如图所示,水平放置的轻弹簧左端固定,小物块P置于光滑水平桌面上的A点并与弹簧的右端接触且不粘连,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=8J.撤去推力后,P沿桌面滑到停在光滑水平面的平板小车Q上,小车的上表面与桌面在同一水平面上.已知P、Q质量分别为m=1Kg、M=4Kg,P与Q的动摩擦因数为μ=0.4.取g=10m/s2,求: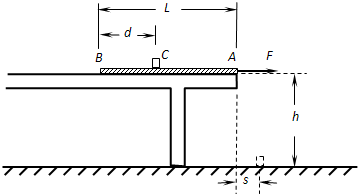 如图所示,水平桌面距地面的高度h=0.80m.可以看成质点的小金属块C的质量m1=0.50kg,放在厚度不计的长木板AB上.木板长L=0.865m,质量m2=0.20kg,木板的A端跟桌面的边缘对齐.小金属块C到木板B端的距离d=0.375m.假定小金属块与木板间、木板与桌面间、小金属块与桌面间的动摩擦因数都相等,其值μ=0.20.现用力将木板水平向右加速抽出,在小金属块从木板上滑下以前,加在木板上的力为水平向右的恒力F.小金属块落到桌面上后,又在桌面上滑动了一段距离,再从桌面边缘飞出落到水平地面上,小金属块落地点到桌边的水平距离s=0.08m.求:
如图所示,水平桌面距地面的高度h=0.80m.可以看成质点的小金属块C的质量m1=0.50kg,放在厚度不计的长木板AB上.木板长L=0.865m,质量m2=0.20kg,木板的A端跟桌面的边缘对齐.小金属块C到木板B端的距离d=0.375m.假定小金属块与木板间、木板与桌面间、小金属块与桌面间的动摩擦因数都相等,其值μ=0.20.现用力将木板水平向右加速抽出,在小金属块从木板上滑下以前,加在木板上的力为水平向右的恒力F.小金属块落到桌面上后,又在桌面上滑动了一段距离,再从桌面边缘飞出落到水平地面上,小金属块落地点到桌边的水平距离s=0.08m.求: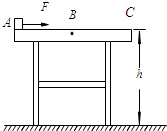 如图所示,水平桌面到地面的高度h=0.8m,质量m=0.2kg的小物块(可以看作质点)放在桌面A端.现对小物块施加一个F=0.8N的水平向右的恒力,小物块从静止开始运动.当它经过桌面上的B点时撤去力F,一段时间后小物块从桌面上的C端飞出,最后落在水平地面上.已知AB=BC=0.5m,小物块在A、B间运动时与桌面间的动摩擦因数μ1=0.2,在B、C间运动时与桌面间的动摩擦因数μ2=0.1.
如图所示,水平桌面到地面的高度h=0.8m,质量m=0.2kg的小物块(可以看作质点)放在桌面A端.现对小物块施加一个F=0.8N的水平向右的恒力,小物块从静止开始运动.当它经过桌面上的B点时撤去力F,一段时间后小物块从桌面上的C端飞出,最后落在水平地面上.已知AB=BC=0.5m,小物块在A、B间运动时与桌面间的动摩擦因数μ1=0.2,在B、C间运动时与桌面间的动摩擦因数μ2=0.1.



