题目内容
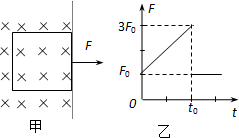（2006?黄浦区模拟）如图甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着磁场边界，t=O时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动，在t0时刻穿出磁场；图乙为外力F随时间变化的图象，若线框质量为m、电阻为R，图象中的F、t0 也为已知量，则在穿出磁场时的速度V=| F0t0 |
| m |
| F0t0 |
| m |
|
|
分析：当t=0时线框的速度为零，没有安培力，根据牛顿第二定律求出加速度a．由运动学公式求出线框刚出磁场时的速度，得到安培力表达式，由牛顿第二定律即可求出B；
解答：解：（1）t=0时刻，线框的速度为零，线框没有感应电流，不受安培力，加速度为a=
①
线框的边长为 L=
at02=
线框刚出磁场时的速度为 v=at0=
②此时线框所受的安培力为FA=BIL，I=
则得 FA=
③
根据牛顿第二定律得 F-FA=ma ④
①②③④联立得：B=
| F0 |
| m |
线框的边长为 L=
| 1 |
| 2 |
| F0t02 |
| 2m |
线框刚出磁场时的速度为 v=at0=
| F0t0 |
| m |
| BLv |
| R |
则得 FA=
| B2L2v |
| R |
根据牛顿第二定律得 F-FA=ma ④
①②③④联立得：B=
|
点评：本题的关键求出安培力，列出牛顿第二定律关于F-t的表达式，考查读图的能力．这里，安培力是联系力学与电磁感应的桥梁．
练习册系列答案
相关题目
（2006?黄浦区模拟）一个用半导体材料制成的电阻器D，其电流I随它两端电压U的关系图象如图（a）所示，将它与两个标准电阻R1、R2并联后接在电压恒为U的电源两端，三个用电器消耗的电功率均为P，现将它们连接成如图（b）所示的电路，接在该电源的两端，设电阻器D和电阻R1、R2消耗的电功率分别是PD、P1、P2，它们之间的大小关系有（ ）
（2006?黄浦区模拟）两列平面简谐波以不同速度沿x方向传播，右图是 t=0 时刻这两列波在长a的区域内的波形．设 t=
（2006?黄浦区模拟）如图所示，粗细不同的两段玻璃管连在一起，粗管上端封闭，细管下端开口，竖直插在大而深的水银槽中，管内封闭有一定质量的空气，两段玻璃管的横截面积之比是2：1．粗管长3cm，细管足够长，管内气柱长2cm，管内外水银面高度差为15cm．现将玻璃管沿竖直方向缓慢上移．（大气压强相当于75cmHg）求：