题目内容
15. 如图所示,B是质量为2m、半径为R的光滑半圆弧槽,放在光滑的水平桌面上.A是质量为3m的细长直杆,在光滑导孔的限制下,A只能上下运动.物块C的质量为m,紧靠B放置.初始时,A杆被夹住,使其下端正好与半圆弧槽内侧的上边缘接触,然后从静止释放A.求:
如图所示,B是质量为2m、半径为R的光滑半圆弧槽,放在光滑的水平桌面上.A是质量为3m的细长直杆,在光滑导孔的限制下,A只能上下运动.物块C的质量为m,紧靠B放置.初始时,A杆被夹住,使其下端正好与半圆弧槽内侧的上边缘接触,然后从静止释放A.求:(1)杆A的下端运动到槽B的最低点时B、C的速度;
(2)杆A的下端经过槽B的最低点后,A能上升的最大高度.
分析 (1)长直杆的下端第一次运动到碗内的最低点时vB=vC,由机械能守恒即可求解;
(2)长直杆的下端上升到的最高点时竖直方向速度为零,根据机械能守恒定律即可求解;
解答 解:(1)最低点时,长直杆在竖直方向的速度为0,BC具有共同速度v,由(整个系统ABC)机械能守恒定律有:
3mgR=$\frac{1}{2}$×3mv2,
所以有:v=vB=vC=$\sqrt{2gR}$,
(2)B、C分离后,杆上升到所能达到的最高点时,AB的速度均为0,AB系统机械能守恒,有:
$\frac{1}{2}$×2mv2=3mgh
解得:h=$\frac{2}{3}$R,
答:(1)杆A的下端运动到槽B的最低点时B、C的速度都为$\sqrt{2gR}$;
(2)杆A的下端经过槽B的最低点后,A能上升的最大高度为$\frac{2}{3}$R.
点评 本题主要考查了机械能守恒定律的直接应用,要知道长直杆的下端第一次运动到碗内的最低点时,A的水平方向速度为零,长直杆的下端上升到的最高点时直杆竖直方向速度为零,难度适中.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
5.下列说法不正确的是( )
| A. | 太阳系中的八大行星有一个共同的轨道焦点 | |
| B. | 行星轨道的半长轴越长,自转周期越大 | |
| C. | 日心说和地心说都是错误的 | |
| D. | 行星在近日点速度最大,远日点速度最小 |
6.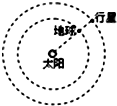 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
 某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )
某行星和地球绕太阳公转的轨道均可视为圆,每过N年,该行星会运行到日地连线的延长线上,如图所示,该行星与地球的公转半径比为( )| A. | ($\frac{N}{N-1}$)${\;}^{\frac{2}{3}}$ | B. | ($\frac{N+1}{N}$)${\;}^{\frac{3}{2}}$ | C. | ($\frac{N}{N-1}$)${\;}^{\frac{3}{2}}$ | D. | ($\frac{N+1}{N}$)${\;}^{\frac{2}{3}}$ |
3.一电器中的变压器可视为理想变压器,它将220V的交变电流改为110V,已知变压器原线圈匝数为1000,则副线圈匝数为( )
| A. | 200 | B. | 500 | C. | 1600 | D. | 3200 |
10.下列说法正确的是( )
| A. | 可利用某些物质在紫外线照射下发出荧光来设计防伪措施 | |
| B. | 根据多普勒效应可以判断遥远天体相对于地球的运动速度 | |
| C. | 光波和无线电波同属电磁波,光波的频率比无线电波的频率低,波长比无线电波的波长大,在真空中传播的速度都约为3.0×108 m/s | |
| D. | “和谐号”动车组高速行驶时,在地面上测得的其车厢长度略微变短 |
20.关于功率,下列认识正确的是( )
| A. | 由P=$\frac{W}{t}$,可知功率越大的机器做的功越多 | |
| B. | 由P=Fv可知汽车发动机功率越大,汽车的速率越大 | |
| C. | 由P=$\frac{W}{t}$可知单位时间内做功越多则功率越大 | |
| D. | 由P=Fv可知机车要想获得大的牵引力,可以放慢速度 |
7.静止在地球上的物体都要随地球一起转动,下列说法正确的是( )
| A. | 它们的线速度大小相同 | B. | 它们的角速度大小相同 | ||
| C. | 它们的向心加速度大小相同 | D. | 它们的向心加速度方向不变 |
5.关于交流电的有效值和最大值,下列说法正确的是( )
| A. | 任何形式的交流电压的有效值是U=$\frac{{U}_{m}}{\sqrt{2}}$的关系 | |
| B. | 只有正弦交流电才具有U=$\frac{{U}_{m}}{\sqrt{2}}$的关系 | |
| C. | 照明电压220V,动力电压380V指的都是有效值 | |
| D. | 交流电压表和电流表测量的是交流电的最大值 |
 在“研究平抛物体的运动”实验中
在“研究平抛物体的运动”实验中