以与水平方向成某一夹角θ斜向上方抛出的物体.只在重力作用下所做的运动叫斜抛运动．(1)试利用牛顿运动定律和运动学规律导出物体在斜抛运动过程中.水平和竖直方向的速度.位移随时间变化的关系式．(2)试证明从水平地面上以一定速率斜向上抛出去的物体.当θ=45°时.落地点和抛出点间的水平距离最大．题目和参考答案——青夏教育精英家教网—

题目内容

以与水平方向成某一夹角θ斜向上方抛出的物体，只在重力作用下所做的运动叫斜抛运动．
（1）试利用牛顿运动定律和运动学规律导出物体在斜抛运动过程中，水平和竖直方向的速度、位移随时间变化的关系式．
（2）试证明从水平地面上以一定速率斜向上抛出去的物体，当θ=45°时，落地点和抛出点间的水平距离最大．

分析：将斜抛运动分解为水平方向和竖直方向，通过水平方向和竖直方向的受力确定两个方向上的运动规律，从而得出水平和竖直方向的速度、位移随时间变化的关系式．
通过两个方向上的运动规律求出落地点和抛出点间的水平距离，通过数学求极值方法得出何时水平距离最大．

解答：解：（1）在水平方向上的初速度v_x=v₀cosθ，不受力，做匀速直线运动，则x=v_xt=v₀tcosθ．
在竖直方向上的初速度v_y0=v₀sinθ，仅受重力做竖直上抛运动，则v_y=v₀sinθ-gt，位移y=v0tsinθ-

gt2．
（2）设初速度为v₀，则竖直方向上初速度v_y=v₀sinθ，则运动的时间t=

2vy

2v0sinθ

，则水平距离x=v0cosθt=

2v02sinθcosθ

v02sin2θ

．
知θ=45°时，sin2θ最大，则落地点和抛出点间的水平距离最大．
答：（1）v_x=v₀cosθ，v_y=v₀sinθ-gt，x=v₀tcosθ，y=v0tsinθ-

gt2．
（2）证明如上所示．

点评：解决本题的关键知道斜抛运动水平方向和竖直方向上的运动规律，结合运动学公式进行求解．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

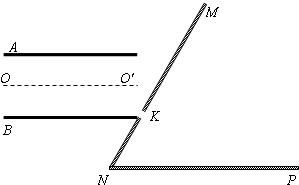如图所示，水平放置的平行金属板A和B间的距离为d，板长L=d，B板的右侧边缘恰好是倾斜挡板NM上的一个小孔K，NM与水平挡板NP成60°角，K与N间的距

=a．现有一质量为m、电荷量为q的带正电的粒子，从AB的中点O以平行于金属板方向OO'的速度v₀射入，不计粒子的重力．现在A、B板上加一恒定电压，则该粒子穿过金属板后恰好穿过小孔K．
（1）求A、B板上所加的恒定电压大小．
（2）求带电粒子到达K点的速度．
（3）在足够长的NM和NP两档板所夹的某一区域存在一垂直纸面向里的匀强磁场，使粒子经过磁场偏转后能垂直打到水平挡板NP上（之前与挡板没有碰撞），求该磁场的磁感应强度的最小值B_min．

在“验证力的平行四边形定则”的实验中，某同学经历了以下实验步骤：

A．用铅笔和直尺在白纸上从O点沿着两细绳方向画直线，按一定标度作出两个力F₁和F₂的图1示，以F₁、F₂为邻边作平行四边形定则，求出F₁、F₂所夹的对角线表示的力F；
B．只用一个测力计，通过细绳把橡皮筋与细绳的连接点拉到同样的位置O；
C．用铅笔记下O点的位置和两条细绳的方向，读出两个弹簧秤的示数；
D．在水平放置的木板上，垫一张白纸并用图钉固定，把橡皮筋的一端固定在板上A点，用两条细绳连接在橡皮筋的另一端，通过细绳同时用两个测力计互成角度地拉橡皮筋，使橡皮筋与细绳的连接点到达某一位置O；
E．记下测力计的读数和细绳方向，按同一标度作出这个力的图示F′，比较合力F′和力F，看它们的大小和方向是否相等；
F．改变两测力计拉力的大小和方向，多次重复实验，根据实验得出结论．
（1）将以上实验步骤按正确顺序排列，应为

DCABEF

（填选项前的字母）．
（2）在物理学中跟力一样，运算时遵守平行四边形定则的物理量还有

位移、速度、加速度、电场强度等

（至少写出两个，要求写名称，不得用符号表示）．
如图2所示，某同学在做“研究匀变速直线运动”实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点的时间间隔T=0.10s，其中s₁=7.05cm、s₂=7.68cm、s₃=8.33cm、s₄=8.95cm、s₅=9.61cm、s₆=10.26cm，则小车运动的加速度计算表达式为a=

(s4+s5+s6)-(s1+s2+s3)

9T2

(s4+s5+s6)-(s1+s2+s3)

如图所示，水平放置的平行金属板A和D间的距离为d，金属板长为L=

d，两板间所加电压为U，D板的右侧边缘恰好是倾斜挡板NM上的一个小孔K，NM与水平挡板NP成60°角，且挡板足够长，K与N间的距离为KN=a．现有一质量为m、电荷量为q的带正电的粒子，从A、D的中点O沿平行于金属板方向OO'以某一速度射入，不计粒子的重力．该粒子穿过金属板后恰好穿

过小孔K：
（1）求该粒子从O点射入时的速度大小v₀；
（2）若两档板所夹的整个区域存在一垂直纸面向外的匀强磁场，粒子经过磁场偏转后能垂直打在水平挡板NP上，求该磁场的磁感应强度的大小B₀；
（3）若磁场方向变为垂直纸面向里，且只存在于两档板所夹间的某一区域内，同样使该粒子经过磁场偏转后能垂直打在水平挡板NP上（之前与挡板没有碰撞），求满足条件的磁感应强度的最小值B_min．

第一部分力＆物体的平衡

第一讲力的处理

一、矢量的运算

1、加法

表达： + = 。

名词：为“和矢量”。

法则：平行四边形法则。如图1所示。

和矢量大小：c = ，其中α为和的夹角。

和矢量方向：在、之间，和夹角β= arcsin

2、减法

表达： = －。

名词：为“被减数矢量”，为“减数矢量”，为“差矢量”。

法则：三角形法则。如图2所示。将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。

差矢量大小：a = ，其中θ为和的夹角。

差矢量的方向可以用正弦定理求得。

一条直线上的矢量运算是平行四边形和三角形法则的特例。

例题：已知质点做匀速率圆周运动，半径为R ，周期为T ，求它在T内和在T内的平均加速度大小。

解说：如图3所示，A到B点对应T的过程，A到C点对应T的过程。这三点的速度矢量分别设为、和。

根据加速度的定义 = 得：= ，=

由于有两处涉及矢量减法，设两个差矢量 = －，= －，根据三角形法则，它们在图3中的大小、方向已绘出（的“三角形”已被拉伸成一条直线）。

本题只关心各矢量的大小，显然：

= = = ，且： = = ， = 2=

所以：= = = ，= = = 。

（学生活动）观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动？

答：否；不是。

3、乘法

矢量的乘法有两种：叉乘和点乘，和代数的乘法有着质的不同。

⑴ 叉乘

表达：× =

名词：称“矢量的叉积”，它是一个新的矢量。

叉积的大小：c = absinα，其中α为和的夹角。意义：的大小对应由和作成的平行四边形的面积。

叉积的方向：垂直和确定的平面，并由右手螺旋定则确定方向，如图4所示。

显然，×≠×，但有：×= －×

⑵ 点乘

表达：· = c

名词：c称“矢量的点积”，它不再是一个矢量，而是一个标量。

点积的大小：c = abcosα，其中α为和的夹角。

二、共点力的合成

1、平行四边形法则与矢量表达式

2、一般平行四边形的合力与分力的求法

余弦定理（或分割成RtΔ）解合力的大小

正弦定理解方向

三、力的分解

1、按效果分解

2、按需要——正交分解

第二讲物体的平衡

一、共点力平衡

1、特征：质心无加速度。

2、条件：Σ = 0 ，或 = 0 ， = 0

例题：如图5所示，长为L 、粗细不均匀的横杆被两根轻绳水平悬挂，绳子与水平方向的夹角在图上已标示，求横杆的重心位置。

解说：直接用三力共点的知识解题，几何关系比较简单。

答案：距棒的左端L/4处。

（学生活动）思考：放在斜面上的均质长方体，按实际情况分析受力，斜面的支持力会通过长方体的重心吗？

解：将各处的支持力归纳成一个N ，则长方体受三个力（G 、f 、N）必共点，由此推知，N不可能通过长方体的重心。正确受力情形如图6所示（通常的受力图是将受力物体看成一个点，这时，N就过重心了）。

答：不会。

二、转动平衡

1、特征：物体无转动加速度。

2、条件：Σ= 0 ，或ΣM₊ =ΣM_-

如果物体静止，肯定会同时满足两种平衡，因此用两种思路均可解题。

3、非共点力的合成

大小和方向：遵从一条直线矢量合成法则。

作用点：先假定一个等效作用点，然后让所有的平行力对这个作用点的和力矩为零。

第三讲习题课

1、如图7所示，在固定的、倾角为α斜面上，有一块可以转动的夹板（β不定），夹板和斜面夹着一个质量为m的光滑均质球体，试求：β取何值时，夹板对球的弹力最小。

解说：法一，平行四边形动态处理。

对球体进行受力分析，然后对平行四边形中的矢量G和N₁进行平移，使它们构成一个三角形，如图8的左图和中图所示。

由于G的大小和方向均不变，而N₁的方向不可变，当β增大导致N₂的方向改变时，N₂的变化和N₁的方向变化如图8的右图所示。

显然，随着β增大，N₁单调减小，而N₂的大小先减小后增大，当N₂垂直N₁时，N₂取极小值，且N_2min = Gsinα。

法二，函数法。

看图8的中间图，对这个三角形用正弦定理，有：

= ，即：N₂ = ，β在0到180°之间取值，N₂的极值讨论是很容易的。

答案：当β= 90°时，甲板的弹力最小。

2、把一个重为G的物体用一个水平推力F压在竖直的足够高的墙壁上，F随时间t的变化规律如图9所示，则在t = 0开始物体所受的摩擦力f的变化图线是图10中的哪一个？

解说：静力学旨在解决静态问题和准静态过程的问题，但本题是一个例外。物体在竖直方向的运动先加速后减速，平衡方程不再适用。如何避开牛顿第二定律，是本题授课时的难点。

静力学的知识，本题在于区分两种摩擦的不同判据。

水平方向合力为零，得：支持力N持续增大。

物体在运动时，滑动摩擦力f = μN ，必持续增大。但物体在静止后静摩擦力f′≡ G ，与N没有关系。

对运动过程加以分析，物体必有加速和减速两个过程。据物理常识，加速时，f ＜ G ，而在减速时f ＞ G 。

答案：B 。

3、如图11所示，一个重量为G的小球套在竖直放置的、半径为R的光滑大环上，另一轻质弹簧的劲度系数为k ，自由长度为L（L＜2R），一端固定在大圆环的顶点A ，另一端与小球相连。环静止平衡时位于大环上的B点。试求弹簧与竖直方向的夹角θ。

解说：平行四边形的三个矢量总是可以平移到一个三角形中去讨论，解三角形的典型思路有三种：①分割成直角三角形（或本来就是直角三角形）；②利用正、余弦定理；③利用力学矢量三角形和某空间位置三角形相似。本题旨在贯彻第三种思路。

分析小球受力→矢量平移，如图12所示，其中F表示弹簧弹力，N表示大环的支持力。

（学生活动）思考：支持力N可不可以沿图12中的反方向？（正交分解看水平方向平衡——不可以。）

容易判断，图中的灰色矢量三角形和空间位置三角形ΔAOB是相似的，所以：

⑴

由胡克定律：F = k（- R） ⑵

几何关系：= 2Rcosθ ⑶

解以上三式即可。

答案：arccos 。

（学生活动）思考：若将弹簧换成劲度系数k′较大的弹簧，其它条件不变，则弹簧弹力怎么变？环的支持力怎么变？

答：变小；不变。

（学生活动）反馈练习：光滑半球固定在水平面上，球心O的正上方有一定滑轮，一根轻绳跨过滑轮将一小球从图13所示的A位置开始缓慢拉至B位置。试判断：在此过程中，绳子的拉力T和球面支持力N怎样变化？

解：和上题完全相同。

答：T变小，N不变。

4、如图14所示，一个半径为R的非均质圆球，其重心不在球心O点，先将它置于水平地面上，平衡时球面上的A点和地面接触；再将它置于倾角为30°的粗糙斜面上，平衡时球面上的B点与斜面接触，已知A到B的圆心角也为30°。试求球体的重心C到球心O的距离。

解说：练习三力共点的应用。

根据在平面上的平衡，可知重心C在OA连线上。根据在斜面上的平衡，支持力、重力和静摩擦力共点，可以画出重心的具体位置。几何计算比较简单。

答案：R 。

（学生活动）反馈练习：静摩擦足够，将长为a 、厚为b的砖块码在倾角为θ的斜面上，最多能码多少块？

解：三力共点知识应用。

答：。

4、两根等长的细线，一端拴在同一悬点O上，另一端各系一个小球，两球的质量分别为m₁和m₂ ，已知两球间存在大小相等、方向相反的斥力而使两线张开一定角度，分别为45和30°，如图15所示。则m₁ : m₂??为多少？

解说：本题考查正弦定理、或力矩平衡解静力学问题。

对两球进行受力分析，并进行矢量平移，如图16所示。

首先注意，图16中的灰色三角形是等腰三角形，两底角相等，设为α。

而且，两球相互作用的斥力方向相反，大小相等，可用同一字母表示，设为F 。

对左边的矢量三角形用正弦定理，有：

= ①

同理，对右边的矢量三角形，有： = ②

解①②两式即可。

答案：1 ：。

（学生活动）思考：解本题是否还有其它的方法？

答：有——将模型看成用轻杆连成的两小球，而将O点看成转轴，两球的重力对O的力矩必然是平衡的。这种方法更直接、简便。

应用：若原题中绳长不等，而是l₁ ：l₂ = 3 ：2 ，其它条件不变，m₁与m₂的比值又将是多少？

解：此时用共点力平衡更加复杂（多一个正弦定理方程），而用力矩平衡则几乎和“思考”完全相同。

答：2 ：3 。

5、如图17所示，一个半径为R的均质金属球上固定着一根长为L的轻质细杆，细杆的左端用铰链与墙壁相连，球下边垫上一块木板后，细杆恰好水平，而木板下面是光滑的水平面。由于金属球和木板之间有摩擦（已知摩擦因素为μ），所以要将木板从球下面向右抽出时，至少需要大小为F的水平拉力。试问：现要将木板继续向左插进一些，至少需要多大的水平推力？

解说：这是一个典型的力矩平衡的例题。

以球和杆为对象，研究其对转轴O的转动平衡，设木板拉出时给球体的摩擦力为f ，支持力为N ，重力为G ，力矩平衡方程为：

f R + N（R + L）= G（R + L） ①

球和板已相对滑动，故：f = μN ②

解①②可得：f =

再看木板的平衡，F = f 。

同理，木板插进去时，球体和木板之间的摩擦f′= = F′。

答案：。

第四讲摩擦角及其它

一、摩擦角

1、全反力：接触面给物体的摩擦力与支持力的合力称全反力，一般用R表示，亦称接触反力。

2、摩擦角：全反力与支持力的最大夹角称摩擦角，一般用φ_m表示。

此时，要么物体已经滑动，必有：φ_m = arctgμ（μ为动摩擦因素），称动摩擦力角；要么物体达到最大运动趋势，必有：φ_ms = arctgμ_s（μ_s为静摩擦因素），称静摩擦角。通常处理为φ_m = φ_ms 。

3、引入全反力和摩擦角的意义：使分析处理物体受力时更方便、更简捷。

二、隔离法与整体法

1、隔离法：当物体对象有两个或两个以上时，有必要各个击破，逐个讲每个个体隔离开来分析处理，称隔离法。

在处理各隔离方程之间的联系时，应注意相互作用力的大小和方向关系。

2、整体法：当各个体均处于平衡状态时，我们可以不顾个体的差异而讲多个对象看成一个整体进行分析处理，称整体法。

应用整体法时应注意“系统”、“内力”和“外力”的涵义。

三、应用

1、物体放在水平面上，用与水平方向成30°的力拉物体时，物体匀速前进。若此力大小不变，改为沿水平方向拉物体，物体仍能匀速前进，求物体与水平面之间的动摩擦因素μ。

解说：这是一个能显示摩擦角解题优越性的题目。可以通过不同解法的比较让学生留下深刻印象。

法一，正交分解。（学生分析受力→列方程→得结果。）

法二，用摩擦角解题。

引进全反力R ，对物体两个平衡状态进行受力分析，再进行矢量平移，得到图18中的左图和中间图（注意：重力G是不变的，而全反力R的方向不变、F的大小不变），φ_m指摩擦角。

再将两图重叠成图18的右图。由于灰色的三角形是一个顶角为30°的等腰三角形，其顶角的角平分线必垂直底边……故有：φ_m = 15°。

最后，μ= tgφ_m 。

答案：0.268 。

（学生活动）思考：如果F的大小是可以选择的，那么能维持物体匀速前进的最小F值是多少？

解：见图18，右图中虚线的长度即F_min ，所以，F_min = Gsinφ_m。

答：Gsin15°（其中G为物体的重量）。

2、如图19所示，质量m = 5kg的物体置于一粗糙斜面上，并用一平行斜面的、大小F = 30N的推力推物体，使物体能够沿斜面向上匀速运动，而斜面体始终静止。已知斜面的质量M = 10kg ，倾角为30°，重力加速度g = 10m/s² ，求地面对斜面体的摩擦力大小。

解说：

本题旨在显示整体法的解题的优越性。

法一，隔离法。简要介绍……

法二，整体法。注意，滑块和斜面随有相对运动，但从平衡的角度看，它们是完全等价的，可以看成一个整体。

做整体的受力分析时，内力不加考虑。受力分析比较简单，列水平方向平衡方程很容易解地面摩擦力。

答案：26.0N 。

（学生活动）地面给斜面体的支持力是多少？

解：略。

答：135N 。

应用：如图20所示，一上表面粗糙的斜面体上放在光滑的水平地面上，斜面的倾角为θ。另一质量为m的滑块恰好能沿斜面匀速下滑。若用一推力F作用在滑块上，使之能沿斜面匀速上滑，且要求斜面体静止不动，就必须施加一个大小为P = 4mgsinθcosθ的水平推力作用于斜面体。使满足题意的这个F的大小和方向。

解说：这是一道难度较大的静力学题，可以动用一切可能的工具解题。

法一：隔离法。

由第一个物理情景易得，斜面于滑块的摩擦因素μ= tgθ

对第二个物理情景，分别隔离滑块和斜面体分析受力，并将F沿斜面、垂直斜面分解成F_x和F_y ，滑块与斜面之间的两对相互作用力只用两个字母表示（N表示正压力和弹力，f表示摩擦力），如图21所示。

对滑块，我们可以考查沿斜面方向和垂直斜面方向的平衡——

F_x = f + mgsinθ

F_y + mgcosθ= N

且 f = μN = Ntgθ

综合以上三式得到：

F_x = F_ytgθ+ 2mgsinθ ①

对斜面体，只看水平方向平衡就行了——

P = fcosθ+ Nsinθ

即：4mgsinθcosθ=μNcosθ+ Nsinθ

代入μ值，化简得：F_y = mgcosθ ②

②代入①可得：F_x = 3mgsinθ

最后由F =解F的大小，由tgα= 解F的方向（设α为F和斜面的夹角）。

答案：大小为F = mg，方向和斜面夹角α= arctg()指向斜面内部。

法二：引入摩擦角和整体法观念。

仍然沿用“法一”中关于F的方向设置（见图21中的α角）。

先看整体的水平方向平衡，有：Fcos(θ- α) = P ⑴

再隔离滑块，分析受力时引进全反力R和摩擦角φ，由于简化后只有三个力（R、mg和F），可以将矢量平移后构成一个三角形，如图22所示。

在图22右边的矢量三角形中，有： = = ⑵

注意：φ= arctgμ= arctg(tgθ) = θ ⑶

解⑴⑵⑶式可得F和α的值。

试题分类