题目内容
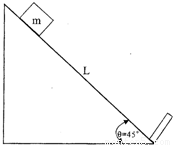
一固定的斜面,倾角为45°,斜面长L=2.0米,在斜面下端有-与斜面垂直的挡板.一质量为m的滑块,从斜面的最高点沿斜面下滑,初速度为零.滑块沿斜面下滑到斜面最低端与挡板发生弹性碰撞(碰撞前后能量没有损失).已知滑块与斜面间的滑动摩擦系数μ=0.2.试求:(1)滑块与挡板发生第1次碰撞时的速度大小及反弹后上升的最大距离?
(2)此滑块从开始运动到与挡板发生第5次碰撞前的过程中运动的总路程.
【答案】分析:(1)对第一次下落的过程运用动能定理列式即可求解速度,向上的过程运动动能定理列式,联立方程即可求解反弹后上升的最大距离;
(2)求出每次上升的距离的通式,从而求出通过的总路程的表达式,带入数据即可求解.
解答:解:(1)由动能定理得mgLsinθ-fL=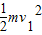 -0①
-0①
且f=μmgcosθ ②
由①②得
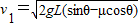 =
=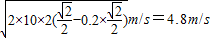
滑块向上运动由动能定理得-mg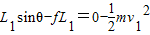 ③
③
由方程①②③得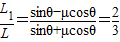
所以反弹后上升的最大距离为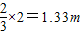
(2)令α=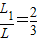 ,则L1=αL
,则L1=αL
同理第2次碰撞后上升的距离为L2=αL1=α2L
第3次碰撞后上升的距离为L3=αL2=α3L
…
第1次碰撞前通过的路程s1=L
第2次碰撞前通过的路程s2=L+2L1=L+2αL
第3次碰撞前通过的路程s3=L+2L1+2L2=L+2αL+2α2L
…
第5次碰撞前通过的路程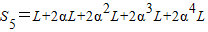 =L(1+2α(
=L(1+2α(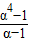 ))
))
代入数值得s5=8.42 m
答:(1)滑块与挡板发生第1次碰撞时的速度大小为4.8m/s,反弹后上升的最大距离为1.33m;
(2)此滑块从开始运动到与挡板发生第5次碰撞前的过程中运动的总路程为8.42m.
点评:本题主要考查了动能定理的直接应用,要求同学们能正确分析物体的运动情况,难度适中.
(2)求出每次上升的距离的通式,从而求出通过的总路程的表达式,带入数据即可求解.
解答:解:(1)由动能定理得mgLsinθ-fL=
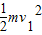 -0①
-0①且f=μmgcosθ ②
由①②得
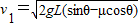 =
=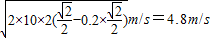
滑块向上运动由动能定理得-mg
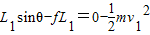 ③
③由方程①②③得
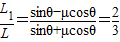
所以反弹后上升的最大距离为
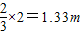
(2)令α=
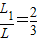 ,则L1=αL
,则L1=αL同理第2次碰撞后上升的距离为L2=αL1=α2L
第3次碰撞后上升的距离为L3=αL2=α3L
…
第1次碰撞前通过的路程s1=L
第2次碰撞前通过的路程s2=L+2L1=L+2αL
第3次碰撞前通过的路程s3=L+2L1+2L2=L+2αL+2α2L
…
第5次碰撞前通过的路程
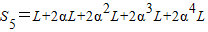 =L(1+2α(
=L(1+2α(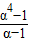 ))
))代入数值得s5=8.42 m
答:(1)滑块与挡板发生第1次碰撞时的速度大小为4.8m/s,反弹后上升的最大距离为1.33m;
(2)此滑块从开始运动到与挡板发生第5次碰撞前的过程中运动的总路程为8.42m.
点评:本题主要考查了动能定理的直接应用,要求同学们能正确分析物体的运动情况,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一固定的斜面,倾角为45°,斜面长L=2.0米,在斜面下端有-与斜面垂直的挡板.一质量为m的滑块,从斜面的最高点沿斜面下滑,初速度为零.滑块沿斜面下滑到斜面最低端与挡板发生弹性碰撞(碰撞前后能量没有损失).已知滑块与斜面间的滑动摩擦系数μ=0.2.试求:
一固定的斜面,倾角为45°,斜面长L=2.0米,在斜面下端有-与斜面垂直的挡板.一质量为m的滑块,从斜面的最高点沿斜面下滑,初速度为零.滑块沿斜面下滑到斜面最低端与挡板发生弹性碰撞(碰撞前后能量没有损失).已知滑块与斜面间的滑动摩擦系数μ=0.2.试求: 一固定的斜面,倾角为θ=45°,斜面长L=3.0m.在斜面的下端有一与斜面垂直的挡板.一质量为m的小滑块可视为质点,从斜面的最高点由静止下滑.滑块与挡板碰撞无机械能损失.滑块与斜面间的动摩擦因数为μ=0.20,求
一固定的斜面,倾角为θ=45°,斜面长L=3.0m.在斜面的下端有一与斜面垂直的挡板.一质量为m的小滑块可视为质点,从斜面的最高点由静止下滑.滑块与挡板碰撞无机械能损失.滑块与斜面间的动摩擦因数为μ=0.20,求

