题目内容
16. 如图所示,在高H的光滑水平平台上,质量m的小物块1以某一水平速度与质量M=2m的静止小物块2正碰,碰后合为一个小物块3;小物块3做平抛运动,恰从光滑圆弧形轨道BC的B点的切线方向进人圆弧形轨道B点的高度h=$\frac{1}{2}$圆弧轨道的圆心O与平台等高,轨道最低点C的切线水平,并与地面上长为L的水平粗糙轨道CD平滑连接;小物块3沿轨道BCD运动与右边墙壁发生碰撞.求:
如图所示,在高H的光滑水平平台上,质量m的小物块1以某一水平速度与质量M=2m的静止小物块2正碰,碰后合为一个小物块3;小物块3做平抛运动,恰从光滑圆弧形轨道BC的B点的切线方向进人圆弧形轨道B点的高度h=$\frac{1}{2}$圆弧轨道的圆心O与平台等高,轨道最低点C的切线水平,并与地面上长为L的水平粗糙轨道CD平滑连接;小物块3沿轨道BCD运动与右边墙壁发生碰撞.求:(1)小物块1的水平速度v0的大小.
(2)小物块3第一次经过C点时地面对它支持力的大小.
(3)若小物块3与墙壁只发生一次碰撞,碰后速度等大反向,没有冲出B点,最后停在轨道CD.上的某点P(P点没画出).设小物块3与轨道CD之间的动摩擦因数为μ,求μ的最小值.
分析 (1)由平抛运动规律可求得A点的速度,结合动量守恒定律求出小物块1的初速度.
(2)由机械能守恒定律及向心力公式可求得支持力的大小;
(3)由功能关系可求得滑动摩擦因素的最小值.
解答 解:(1)因h=$\frac{1}{2}H$,故∠BOC=60°,设小物块3的水平速度为v,从A到B的时间为t,则有:
$H-h=\frac{1}{2}g{t}^{2}$,
$\frac{gt}{v}=tan60°$,
解得:v=$\sqrt{\frac{gH}{3}}$.
m与M发生相互作用,动量守恒,规定小物块1的方向为正方向,有:
mv0=(M+m)v,
解得:${v}_{0}=\sqrt{3gH}$.
(2)小物块3由A到C,机械能守恒,有
$\frac{1}{2}(m+M){v}^{2}+(m+M)gH=\frac{1}{2}(m+M){{v}_{C}}^{2}$,
解得:${v}_{C}=\sqrt{\frac{7gH}{3}}$,
在C点,由牛顿第二定律有:
$N-(m+M)g=(m+M)\frac{{{v}_{C}}^{2}}{H}$,
解得:N=10mg.
(3)设小物块3在水平轨道上通过的路程为s,根据题意,路程的最大值是:smax=3L,
由功能关系得:$\frac{1}{2}(m+M){v}^{2}+(M+m)gH={μ}_{min}(m+M)g•3L$,
解得:${μ}_{min}=\frac{7H}{18L}$.
答:(1)小物块1的水平速度v0的大小为$\sqrt{3gH}$.
(2)小物块3第一次经过C点时地面对它支持力的大小为10mg.
(3)μ的最小值为$\frac{7H}{18L}$.
点评 本题考查了功能关系及平抛运动规律,要注意正确分析物理过程,明确对应的物理规律,才能准确列式求解.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案 如图所示,在光滑的水平直线导轨上,有质量分别为2m和m、带电量分别为2q、q的两个小球A、B正相向运动,某时刻A、B两球的速度大小分别为vA、vB.由于静电斥力作用,A球先开始反向运动,它们不会相碰,最终两球都反向运动.则( )
如图所示,在光滑的水平直线导轨上,有质量分别为2m和m、带电量分别为2q、q的两个小球A、B正相向运动,某时刻A、B两球的速度大小分别为vA、vB.由于静电斥力作用,A球先开始反向运动,它们不会相碰,最终两球都反向运动.则( )| A. | vA>vB | B. | vA<$\frac{1}{2}$vB | C. | vA=$\frac{1}{2}$v | D. | vB>vA>$\frac{1}{2}$vB |
| A. | 黑体辐射电磁波的强度按波长的分布只与黑体的温度有关 | |
| B. | 对于同种金属产生光电效应时,逸出光电子的最大初动能 Ek与照射光的频率成线性关系 | |
| C. | 一块纯净的放射性元素的矿石,经过一个半衰期以后,它的总质量仅剩下一半 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子的能量也减小了 | |
| E. | 将核子束缚在原子核内的核力,是不同于万有引力和电磁力的另一种相互作用 |
| A. | 冥王星的卫星查龙(charon)围绕冥王星做匀速圆周运动的线速度和轨道半径 | |
| B. | 冥王星的卫星查龙(charon)围绕冥王星做圆周运动的加速度和冥王星的半径 | |
| C. | 冥王星围绕太阳运转的线速度和冥王星的半径 | |
| D. | 冥王星围绕太阳运转的周期和轨道半径 |
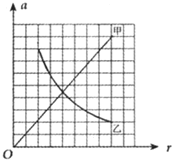 甲、乙两球做匀速圆周运动,向心加速度a 随半径r变化的关系如图所示,甲为一倾斜直线,乙为双曲线的一部分.有以下4种说法:
甲、乙两球做匀速圆周运动,向心加速度a 随半径r变化的关系如图所示,甲为一倾斜直线,乙为双曲线的一部分.有以下4种说法:①甲球运动时的线速度大小保持不变
②甲球运动时的角速度大小保持不变
③乙球运动时的线速度大小保持不变
④乙球运动时的角速度大小保持不变
由图象可以知道,说法正确的是( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②④ |
 如图所示,从水平地面上的A点,以速度v1在竖直平面内抛出一小球,v1与地面成θ角.小球恰好以v2的速度水平打在墙上的B点,不计空气阻力,则下面说法中正确的是( )
如图所示,从水平地面上的A点,以速度v1在竖直平面内抛出一小球,v1与地面成θ角.小球恰好以v2的速度水平打在墙上的B点,不计空气阻力,则下面说法中正确的是( )| A. | 在A点,仅改变θ角的大小,小球仍可能水平打在墙上的B点 | |
| B. | 在A点,以大小等于v2的速度朝墙抛向小球,它也可能水平打在墙上的B点 | |
| C. | 在B点水平向左抛出小球,让它落回地面上A点,则抛出速度大小一定等于v2 | |
| D. | 在B点以大小为v1的速度水平向左抛出小球,则它可能落在地面上的A点 |
 如图所示,两平行金属板竖直放置,板上A、B两孔正好水平相对,板间电压为500V.一个动能为400eV的带电粒子电荷量大小为e,从A孔沿垂直板方向射入电场中.经过一段时间粒子离开电场,则粒子离开电场时的动能大小可能为( )
如图所示,两平行金属板竖直放置,板上A、B两孔正好水平相对,板间电压为500V.一个动能为400eV的带电粒子电荷量大小为e,从A孔沿垂直板方向射入电场中.经过一段时间粒子离开电场,则粒子离开电场时的动能大小可能为( )| A. | 900eV | B. | 500eV | C. | 400eV | D. | 100eV |
A.干电池(待测)
B.定值电阻R1=480Ω
C.滑动变阻器R2(0~15Ω)
D.电流表A1 (内阻0.3Ω,量程0.6A)
E.电流表A2 (内阻0.1Ω,量程3A)
F.电流表A3 (内阻20Ω,量程300mA)
G.电流表A4 (内阻20Ω,量程3mA)
H.开关K
J.导线若干
为了方便、准确地测出电源电动势和内电阻.

①电路图中a处电流表应选择A4,b处电流表应选择A1.
②表是某次实验中测出五组数据,请在图2中画出Ia-Ib图.
| 1 | 2 | 3 | 4 | 5 | |
| Ia(mA) | 2.80 | 2.60 | 2.50 | 2.20 | 2.00 |
| Ib(A) | 0.12 | 0.24 | 0.27 | 0.45 | 0.57 |
 长为l的轻杆的一端固定一小球,绕另一端O在竖直平面内以角速度ω沿逆时针方向匀速转动,如图所示.已知小球的质量为m,重力加速度为g,当小球处于图示位置(轻杆处于水平)时,轻杆对小球的作用力大小为( )
长为l的轻杆的一端固定一小球,绕另一端O在竖直平面内以角速度ω沿逆时针方向匀速转动,如图所示.已知小球的质量为m,重力加速度为g,当小球处于图示位置(轻杆处于水平)时,轻杆对小球的作用力大小为( )| A. | m$\sqrt{{ω}^{4}{l}^{2}+{g}^{2}}$ | B. | m$\sqrt{{ω}^{4}{l}^{2}-{g}^{2}}$ | C. | mω2l | D. | 0 |