题目内容
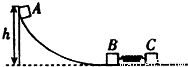
如图所示,一轻质弹簧的一端固定在滑块B上,另一端与滑块C接触但未连接,该整体静置在光滑水平面上.现有一滑块A从光滑曲面上离水平面h高处由静止开始滑下,与滑块B发生碰撞(时间极短)并粘在一起压缩弹簧推动滑块C向前运动,经过一段时间,滑块C脱离弹簧,继续在水平面上做匀速运动.已知mA=mB=m,mC=2m,求:(1)滑块A与滑块B碰撞时的速度v1大小;
(2)滑块A与滑块B碰撞结束瞬间它们的速度v2的大小;
(3)滑块C在水平面上匀速运动的速度的大小.
【答案】分析:(1)一滑块A从光滑曲面上离水平面h高处由静止开始滑下,根据机械能守恒定律求出滑块A与滑块B碰撞时的速度
(2)A与B碰撞前后根据动量守恒定律求解
(3)A、B、C看成整体,由动量守恒定律和机械能守恒定律列出等式求解.
解答:解:(1)设A与B碰撞时的速度大小为v1,根据机械能守恒定律得

∴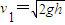
(2)A与B碰撞后瞬间速度大小为v2.
根据动量守恒定律:
mv1=2mv2
∴
(3)设C匀速运动的速度为vc,此时AB的速度为vAB,
由动量守恒定律和机械能守恒定律得
2mv2=2mvAB+2mvc

由以上两式解得:
答:(1)滑块A与滑块B碰撞时的速度是 ;
;
(2)滑块A与滑块B碰撞结束瞬间它们的速度是 ;
;
(3)滑块C在水平面上匀速运动的速度的大小是 .
.
点评:利用动量守恒定律解题,一定注意状态的变化和状态的分析.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.
(2)A与B碰撞前后根据动量守恒定律求解
(3)A、B、C看成整体,由动量守恒定律和机械能守恒定律列出等式求解.
解答:解:(1)设A与B碰撞时的速度大小为v1,根据机械能守恒定律得

∴
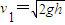
(2)A与B碰撞后瞬间速度大小为v2.
根据动量守恒定律:
mv1=2mv2
∴

(3)设C匀速运动的速度为vc,此时AB的速度为vAB,
由动量守恒定律和机械能守恒定律得
2mv2=2mvAB+2mvc

由以上两式解得:

答:(1)滑块A与滑块B碰撞时的速度是
 ;
;(2)滑块A与滑块B碰撞结束瞬间它们的速度是
 ;
;(3)滑块C在水平面上匀速运动的速度的大小是
 .
.点评:利用动量守恒定律解题,一定注意状态的变化和状态的分析.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( )
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( ) 如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( )
如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( ) 如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )
如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )