题目内容
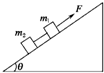 如图所示,有两个相同材料物体组成的连接体在斜面上运动,当作用力F一定时,m2所受绳的拉力( )
如图所示,有两个相同材料物体组成的连接体在斜面上运动,当作用力F一定时,m2所受绳的拉力( )分析:对整体分析,运用牛顿第二定律求出整体的加速度,隔离对m2分析,运用牛顿第二定律求出拉力的大小,判断与什么因素有关.
解答:解:对整体分析,根据牛顿第二定律得,a=
=
-gsinθ-μgcosθ.
隔离对m2分析,有:T-m2gsinθ-μm2gcosθ=m2a,解得T=
.知绳子的拉力与θ无关,与动摩擦因数无关,与运动状态无关,仅与两物体的质量有关.故D正确,A、B、C错误.
故选D.
| F-(m1+m2)gsinθ-μ(m1+m2)gcosθ |
| m1+m2 |
| F |
| m1+m2 |
隔离对m2分析,有:T-m2gsinθ-μm2gcosθ=m2a,解得T=
| m2F |
| m1+m2 |
故选D.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则可以断定( )
如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则可以断定( )| A、A粒子的初动能是B粒子的2倍 | B、A粒子在C点的偏向角的正弦值是B粒子的2倍 | C、A、B两粒子到达C点时的动能可能相同 | D、如果仅将加在两极板间的电压加倍,A、B两粒子到达下极板时仍为同一点D(图中未画出) |
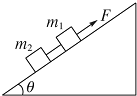 如图所示,有两个相同材料物体组成的连接体在斜面上向上运动,当作用力F一定时,m2所受绳的拉力( )
如图所示,有两个相同材料物体组成的连接体在斜面上向上运动,当作用力F一定时,m2所受绳的拉力( )| A、与θ有关 | ||
| B、与斜面动摩擦因数无关 | ||
| C、与系统运动状态无关 | ||
D、FT=
|
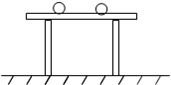 如图所示,有两个相同质量可看成质点的铁球和木球,放置在同一张水平桌面上.若选定地面为零势能参考平面,则比较这两个球的重力势能的大小,正确的是( )
如图所示,有两个相同质量可看成质点的铁球和木球,放置在同一张水平桌面上.若选定地面为零势能参考平面,则比较这两个球的重力势能的大小,正确的是( ) 如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则不可以判定的是( )
如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则不可以判定的是( )