题目内容
 如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则可以断定( )
如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则可以断定( )| A、A粒子的初动能是B粒子的2倍 | B、A粒子在C点的偏向角的正弦值是B粒子的2倍 | C、A、B两粒子到达C点时的动能可能相同 | D、如果仅将加在两极板间的电压加倍,A、B两粒子到达下极板时仍为同一点D(图中未画出) |
分析:带电粒子垂直进入电场后做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动.根据牛顿第二定律和运动学公式推导出偏转距离与初动能的关系、偏向角正弦值与分析初动能的关系.根据推论:带电粒子在匀强电场中做类平抛运动,射出电场后,速度反向延长线交水平位移的中点,研究两粒子在C点的偏向角的正切值的关系.根据电场力做功,由动能定理分析两粒子到达C点时的动能关系.如果仅将加在两极板间的电压加倍,A、B两粒子不能到达下极板上同一点D.
解答:解:A、设平行金属板长为l,板间距离为d,场强为E,则运用运动的分解法研究得到:
水平方向:l=v0t
竖直方向:y=
at2
a=
联立得到,y=
=
由图看出,两个粒子的水平位移都等于板长l,q、E相同,y之比为yA:yB=1:2,初动能Ek与y成反比,可以判定A粒子的初动能是B粒子的2倍.故A正确.
B、设A、B两粒子在C点的偏向角分别为α、β,根据推论:带电粒子在匀强电场中做类平抛运动,射出电场后,速度反向延长线交水平位移的中点,得到:
tanα=
=
,tanβ=
=2
,则tanα=2tanβ,可见A的偏向角大于B的偏向角,α、β都是锐角,根据数学知识判定A粒子在C点的偏向角的正弦值不是B粒子的两倍.故B错误.
C、根据动能定理得,Ek′-Ek=qEy,得粒子到达C点时的动能为Ek′=Ek+qEy,A粒子的初动能Ek大,y较小,而,B粒子的初动能Ek小,y较大,A、B两粒子到达C点时的动能Ek′可能相同.故C正确.
D、如果仅将加在两极板间的电压加倍,由上得到y=
=
,A、B两粒子到达下极板时y之比为yA:yB=1:2,电压U加倍时,x仍相等,两粒子到达下极板时仍为同一点D.故D正确.
故选:ACD.
水平方向:l=v0t
竖直方向:y=
| 1 |
| 2 |
a=
| qE |
| m |
联立得到,y=
q
| ||
2m
|
| qEl2 |
| 4Ek |
由图看出,两个粒子的水平位移都等于板长l,q、E相同,y之比为yA:yB=1:2,初动能Ek与y成反比,可以判定A粒子的初动能是B粒子的2倍.故A正确.
B、设A、B两粒子在C点的偏向角分别为α、β,根据推论:带电粒子在匀强电场中做类平抛运动,射出电场后,速度反向延长线交水平位移的中点,得到:
tanα=
| ||
|
| d |
| l |
| d | ||
|
| d |
| l |
C、根据动能定理得,Ek′-Ek=qEy,得粒子到达C点时的动能为Ek′=Ek+qEy,A粒子的初动能Ek大,y较小,而,B粒子的初动能Ek小,y较大,A、B两粒子到达C点时的动能Ek′可能相同.故C正确.
D、如果仅将加在两极板间的电压加倍,由上得到y=
q
| ||
2m
|
q
| ||
2dm
|
故选:ACD.
点评:本题运用运动的分解法研究类平抛运动,要用到推论、动能定理、牛顿第二定律等多个规律和结论,有一定的难度.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
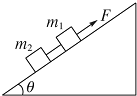 如图所示,有两个相同材料物体组成的连接体在斜面上向上运动,当作用力F一定时,m2所受绳的拉力( )
如图所示,有两个相同材料物体组成的连接体在斜面上向上运动,当作用力F一定时,m2所受绳的拉力( )| A、与θ有关 | ||
| B、与斜面动摩擦因数无关 | ||
| C、与系统运动状态无关 | ||
D、FT=
|
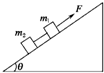 如图所示,有两个相同材料物体组成的连接体在斜面上运动,当作用力F一定时,m2所受绳的拉力( )
如图所示,有两个相同材料物体组成的连接体在斜面上运动,当作用力F一定时,m2所受绳的拉力( )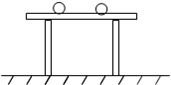 如图所示,有两个相同质量可看成质点的铁球和木球,放置在同一张水平桌面上.若选定地面为零势能参考平面,则比较这两个球的重力势能的大小,正确的是( )
如图所示,有两个相同质量可看成质点的铁球和木球,放置在同一张水平桌面上.若选定地面为零势能参考平面,则比较这两个球的重力势能的大小,正确的是( ) 如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则不可以判定的是( )
如图所示,有两个相同的带电粒子A、B,分别从平行板间左侧中点和贴近上极板左端处以不同的初速度垂直于电场方向进入电场,它们恰好都打在下极板右端处的C点,若不计重力,则不可以判定的是( )