题目内容
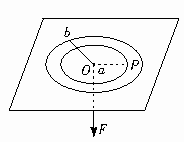
如图所示，在水平面的光滑平板上有一个质量为M的质点P，与穿过中央小孔O的轻绳一端连接，平板与小孔都是光滑的，现用手拉着绳子下端使质点做半径为a，角速度为ω1的匀速圆周运动，若绳子迅速放松至某一长度b而拉紧，质点就能在以半径为b的圆周上做匀速圆周运动，求质点由半径a到b所需的时间及质点在半径为b的圆周上运动的角速度．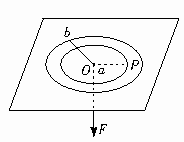
答案：
解析：
提示：
解析：
答案： ；
解析：质点P在半径为a的圆周上以角速度ω1做匀速圆周运动，其线速度为va＝ ω1a
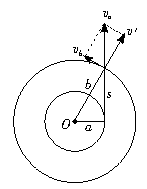
突然松开绳后，向心力消失，质点沿切线方向飞出，沿光滑平板以va做匀速直线运动，直到线被拉直.如图 所示，质点做匀速直线运动的位移为t＝ 当线刚被拉直时，质点P的速度为va，将这一速度分解为垂直于绳的速度vb和沿绳的速度v′，在绳绷紧的过程中沿绳的速度v′减为零，垂直于绳的速度vb不变，质点就以vb沿着半径为b的圆周做匀速直线运动，根据相似三角形，有 将va＝ω1a和vb＝ω2b代入上式所以ω2＝ |
＝
．提示：
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图所示，在水平地面上有一个长L=1.5m，高h=0.8m的长方体木箱，其质量为M=1kg，与地面的动摩擦因数μ=0.3．在它的上表面的左端放有一质量为m=4kg的小铁块，铁块与木箱的摩擦不计．开始它们均静止．现对木箱施加一水平向左的恒力F=27N．（g=10m/s2）问：
选做题
如图所示，在水平地面上放置两个物体A、B，已知A、B与地面的最大静摩擦力分别为10N和5N，若沿水平向右的方向用F=9N的力推物体A时，A、B受到地面的摩擦力分别为（ ）