��Ŀ����
8�� ��ͼ��ʾ���ֲڵ�������һ��Ǧ�=30��⻬б�棬б�涥�˰�װһ�����֣�С���A��B���������Ӳ�������֣����ƻ��ֵ�������Ħ��������ʼʱ�̣�С���A��Bλ��ͬһ�߶ȴ���ǡ�ô��ھ�ֹ״̬������������A���䡢B��б���»���б�澲ֹ��������Ӽ�������������ţ�����˵����ȷ���ǣ�������
��ͼ��ʾ���ֲڵ�������һ��Ǧ�=30��⻬б�棬б�涥�˰�װһ�����֣�С���A��B���������Ӳ�������֣����ƻ��ֵ�������Ħ��������ʼʱ�̣�С���A��Bλ��ͬһ�߶ȴ���ǡ�ô��ھ�ֹ״̬������������A���䡢B��б���»���б�澲ֹ��������Ӽ�������������ţ�����˵����ȷ���ǣ�������| A�� | ���A��B������� | B�� | ���A��Bͬʱ��� | ||
| C�� | �����ܵ�б�������Ħ���� | D�� | ������ŵ�ʱ������˲�书����ͬ |
���� ����ƽ��ó�����������Ĺ�ϵ��ץס���ʱ�ٶȴ�С��ȣ����˲ʱ���ʵĹ�ʽ�Ƚ����ʱ���������˲ʱ���ʵĴ�С��ϵ�����ݼ��ٶȲ�ͬ�Ƚ��˶���ʱ�䣮ͨ����б�������������жϵ����б���Ħ������
��� �⣺A���տ�ʼAB���ھ�ֹ״̬��������mBgsin��=mAg����mB��mA����A����
B����Ϊ��ص��ٶȴ�С��ȣ����ٶȲ��ȣ������ٶ�ʱ�乫ʽ֪���˶���ʱ�䲻�ȣ���B����
C����ΪB��б����б�����·���ѹ����б���������˶������ƣ����Ե����б�����ҵľ�Ħ����������ţ�ٵ������ɣ������ܵ�б�������Ħ��������C��ȷ��
D������������A�������䣬B��б���»���AB��ֻ���������������ݻ�е���غ㶨�ɵã�mgh=$\frac{1}{2}m{v}_{\;}^{2}$���ٶȴ�Сv=$\sqrt{2gh}$����A�����Ĺ���${P}_{A}^{\;}={m}_{A}^{\;}g\sqrt{2gh}$��B�����Ĺ���${P}_{B}^{\;}={m}_{B}^{\;}g\sqrt{2gh}sin��$����֪PA=PB����D��ȷ��
��ѡ��CD
���� ���⿼���˹�����ƽ�⡢��е���غ㡢���ʵĻ������ã�ͨ��ƽ��ó�A��B��������ϵ�ǽ������Ĺؼ���ע��˲ʱ���ʵ��������ٶ��Լ�֮��н����ҵij˻���

 ��ҵ����ϵ�д�
��ҵ����ϵ�д�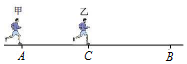 ��ͼ��ʾ���״�A���ɾ�ֹ�ȼ�������B�أ�����ǰ������Ϊ1mʱ���ҴӾ�A��5m����C���ɾ�ֹ�������ҵļ��ٶ���ļ��ٶ���ͬ��������ͬʱ����B�أ���A��B���ؾ���Ϊ��������
��ͼ��ʾ���״�A���ɾ�ֹ�ȼ�������B�أ�����ǰ������Ϊ1mʱ���ҴӾ�A��5m����C���ɾ�ֹ�������ҵļ��ٶ���ļ��ٶ���ͬ��������ͬʱ����B�أ���A��B���ؾ���Ϊ��������| A�� | 6m | B�� | 9m | C�� | 12m | D�� | 15m |
 ��������L�������̶�����E��F�����������С�ֱ���QE��QF�������ǹ�ͬ�γɵĵ糡�У���һ���糡����ͼ��ʵ����ʾ��ʵ���ϵļ�ͷ��ʾ�糡�ߵķ��糡���ϱ����M��N���㣬����N���������EF����ƽ�У��ҡ�NEF����NFE��������
��������L�������̶�����E��F�����������С�ֱ���QE��QF�������ǹ�ͬ�γɵĵ糡�У���һ���糡����ͼ��ʵ����ʾ��ʵ���ϵļ�ͷ��ʾ�糡�ߵķ��糡���ϱ����M��N���㣬����N���������EF����ƽ�У��ҡ�NEF����NFE��������| A�� | E�����磬F�����磬��QE��QF | |
| B�� | ��M���ɾ�ֹ�ͷ�һ������ļ����ɣ������ɽ��ص糡���˶���N�� | |
| C�� | ��N��ĵ�������EF���ߴ�ֱ | |
| D�� | ����������M��ĵ����ܴ�����N��ĵ����� |
 ��ͼ��ʾ���綯��ΪE�����費�Ƶĵ�Դ���������ݺ�����������ӣ�ֻ���Ͽ���S1���������ݶ�����������������ٺ���S2�������б�����ȷ���ǣ�������
��ͼ��ʾ���綯��ΪE�����費�Ƶĵ�Դ���������ݺ�����������ӣ�ֻ���Ͽ���S1���������ݶ�����������������ٺ���S2�������б�����ȷ���ǣ�������| A�� | ��Դ������ʼ�С | B�� | L1���ĵĹ��ʼ�С | ||
| C�� | ͨ��R1�ϵĵ������� | D�� | ͨ��R3�ϵĵ������� |
 ��ͬһˮƽֱ���ϵ���λ�÷ֱ���ͬ�����׳���С�� A ��B�����˶��켣��ͼ��ʾ�����ƿ���������Ҫʹ�����ڿ�������������루������
��ͬһˮƽֱ���ϵ���λ�÷ֱ���ͬ�����׳���С�� A ��B�����˶��켣��ͼ��ʾ�����ƿ���������Ҫʹ�����ڿ�������������루������| A�� | ���׳�A�� | B�� | ���׳�B�� | ||
| C�� | ͬʱ�׳����� | D�� | A��ij��ٶȵ���B��ij��ٶ� |
 ��һ�ռ�ֲ��ĵ糡����ͼ��ʾΪ����һ���糡�ߣ�A��B��CΪ�糡���ϵ����㣬��ͷ����Ϊ��������߷���������˵����ȷ���ǣ�������
��һ�ռ�ֲ��ĵ糡����ͼ��ʾΪ����һ���糡�ߣ�A��B��CΪ�糡���ϵ����㣬��ͷ����Ϊ��������߷���������˵����ȷ���ǣ�������| A�� | A��ij�ǿ����С��C��ij�ǿ | |
| B�� | A��B��C��������߷���Ϊ��̽����ڸ�λ�õ��������� | |
| C�� | �����ɴ�A���ص糡���˶���C�㣬�������������ж� | |
| D�� | �����ɽ��ܵ糡��������A����ֹ�ͷź�����ظõ糡���˶� |
| A�� | ���ӵ����ʼӱ������ڼ��� | |
| B�� | �������ʲ��䣬����뾶���� | |
| C�� | ���ӵ����ʼ��룬����뾶��Ϊԭ����$\frac{1}{2}$ | |
| D�� | �������ʲ��䣬���ڼ��� |
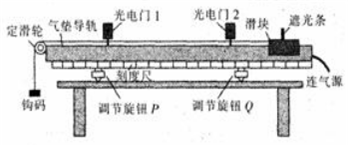 ijͬѧ������ͼ��ʾ�����浼��װ����֤��е���غ㶨�ɣ������浼���ϰ�װ����ͬ���������1��2�������Ϲ̶�һ�ڹ�����������ϸ���ƹ����ʶ������빳��������
ijͬѧ������ͼ��ʾ�����浼��װ����֤��е���غ㶨�ɣ������浼���ϰ�װ����ͬ���������1��2�������Ϲ̶�һ�ڹ�����������ϸ���ƹ����ʶ������빳��������