题目内容
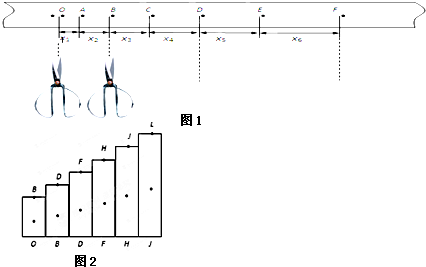
某同学利用打点计时器研究做匀加速直线运动小车的运动情况，图1所示为该同学实验时打出的一条纸带中的部分计数点（后面计数点未画出），相邻计数点间有4个点迹未画出．（打点计时器每隔0.02s打出一个点）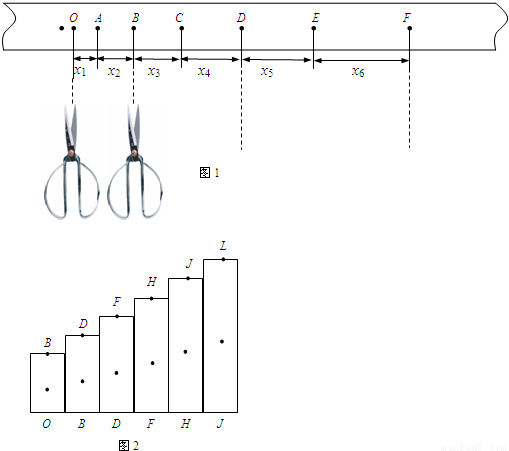
（1）为研究小车的运动，此同学用剪刀沿虚线方向把纸带上OB、BD、DF…等各段纸带剪下，将剪下的纸带一端对齐，按顺序贴好，如图2所示．简要说明怎样判断此小车是否做匀变速直线运动．
方法：______．
（2）在图2中x1=7.05cm、x2=7.68cm、x3=8.31cm、x4=8.94cm、x5=9.57cm、x6=10.20cm，则打下点迹A时，小车运动的速度大小是______m/s，小车运动的加速度大小是______m/s2．（本小题计算结果保留两位有效数字）
【答案】分析：（1）纸带的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，最后得出结论纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比．
（2）匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，由此可求出E点的速度，根据逐差法求出加速度，根据vt=v+at，可求出F点的速度．
解答：解：（1）它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，最后得出结论纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比，因此图2中的B、D、F、H、J、L，各点连起来恰好为一直线，说明每相邻两个纸袋相差的长度相等，即△x=aT2，所以说明小车做匀变速直线运动．
故答案为：连接纸带左上角（上方中点或纸带中点）为一条直线或每条纸带比前一条纸带长度增加量相等．
（2）匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，由此可得：
根据匀变速直线运动的推论△x=aT2，有：
x6-x3=3a1T2 ①
x5-x2=3a2T2 ②
x4-x1=3a3T2 ③
④
联立①②③④解得：
≈0.63m/s2．
故答案为：0.74，0.63．
点评：本题借助实验考查了匀变速直线的规律以及推论的应用，在平时练习中要加强基础知识的理解与应用，提高解决问题能力．
（2）匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，由此可求出E点的速度，根据逐差法求出加速度，根据vt=v+at，可求出F点的速度．
解答：解：（1）它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，最后得出结论纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比，因此图2中的B、D、F、H、J、L，各点连起来恰好为一直线，说明每相邻两个纸袋相差的长度相等，即△x=aT2，所以说明小车做匀变速直线运动．
故答案为：连接纸带左上角（上方中点或纸带中点）为一条直线或每条纸带比前一条纸带长度增加量相等．
（2）匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，由此可得：
根据匀变速直线运动的推论△x=aT2，有：
x6-x3=3a1T2 ①
x5-x2=3a2T2 ②
x4-x1=3a3T2 ③
④联立①②③④解得：
≈0.63m/s2．故答案为：0.74，0.63．
点评：本题借助实验考查了匀变速直线的规律以及推论的应用，在平时练习中要加强基础知识的理解与应用，提高解决问题能力．
练习册系列答案
阅读快车系列答案
相关题目
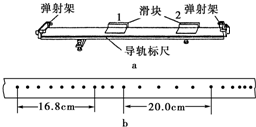（2009?肇庆一模）某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验．气垫导轨装置如图a所示，所用的气垫导轨装置由导轨、滑块、弹射架等组成．在空腔导轨的两个工作面上均匀分布着一定数量的小孔，向导轨空腔内不断通入压缩空气，空气会从小孔中喷出，使滑块稳定地漂浮在导轨上，这样就大大减小了因滑块和导轨之间的摩擦而引起的误差．
