题目内容
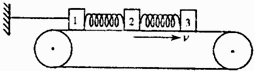
 两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在b弹簧的p端向右拉动弹簧,已知a弹簧的伸长量为L,则
两个劲度系数分别为k1和k2的轻质弹簧a、b串接在一起,a弹簧的一端固定在墙上,如图所示.开始时弹簧均处于原长状态,现用水平力作用在b弹簧的p端向右拉动弹簧,已知a弹簧的伸长量为L,则
- A.b弹簧的伸长量也为L
- B.b弹簧的伸长量为

- C.P端向右移运动的距离为2L
- D.P端向右移运动的距离为

B
分析:两根轻弹簧串联,弹力大小相等,根据胡克定律分析伸长量的大小.P端向右移动的距离等于两根弹簧伸长量之和.
解答:AB、两根轻弹簧串联,弹力大小相等,根据胡克定律F=kx得x与k成反比,则得b弹簧的伸长量为 .故A错误,B正确.
.故A错误,B正确.
CD、P端向右移动的距离等于两根弹簧伸长量之和,即为L+ =(1+
=(1+ )L,故CD错误.
)L,故CD错误.
故选B
点评:本题关键要知道两弹簧的弹力大小相等,掌握胡克定律,并能求出弹簧的伸长量.
分析:两根轻弹簧串联,弹力大小相等,根据胡克定律分析伸长量的大小.P端向右移动的距离等于两根弹簧伸长量之和.
解答:AB、两根轻弹簧串联,弹力大小相等,根据胡克定律F=kx得x与k成反比,则得b弹簧的伸长量为
 .故A错误,B正确.
.故A错误,B正确.CD、P端向右移动的距离等于两根弹簧伸长量之和,即为L+
 =(1+
=(1+ )L,故CD错误.
)L,故CD错误.故选B
点评:本题关键要知道两弹簧的弹力大小相等,掌握胡克定律,并能求出弹簧的伸长量.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
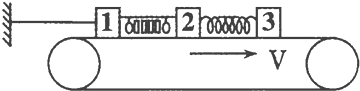

 ,现用水平细绳将木块I固定在左边的墙上,传送带按图示方向匀速运动,则( )
,现用水平细绳将木块I固定在左边的墙上,传送带按图示方向匀速运动,则( )