Question

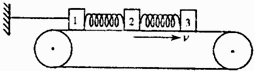
如图所示，在水平传送带上有三个质量分别为m₁、m₂、m₃的木块1、2、3（可视为质点），中间分别用原长均为L、劲度系数均为k的轻弹簧连接，木块与传送带间的动摩擦因数μ．现用水平细绳将木块1固定在左边的墙上，让传送带按图示方向匀速运动，当三个木块达到平衡后，1、2两木块间的距离是（　　）

A．L+ μm2g k	B．L+ μ(m2+m3)g k
C．L+ μ(m1+m2+m3)g k	D．L+ μm1g k

Answer 1

当三木块达到平衡状态后，对木块3进行受力分析，可知2和3间弹簧的弹力等于木块3所受的滑动摩擦力，即：
μm₃g=kx₃，解得2和3间弹簧伸长量为：x₃=

μm3g

k

；
同理以2木块为研究对象得：kx₂=kx₃+μm₂g，即1和2间弹簧的伸长量为：x₂=

μm3g+μm2g

k

=

μ(m2+m3)g

k

，
1、2两木块之间的距离等于弹簧的原长加上伸长量，即得L+

μ(m2+m3)g

k

，选项B正确．
故选B