题目内容
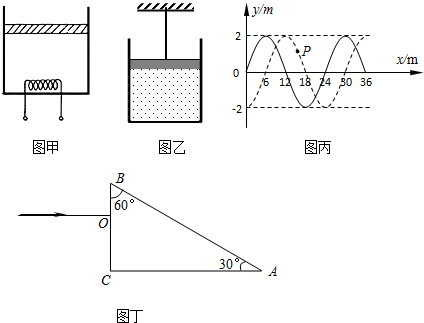
 如图实线是一列简谐横波在t1=0时的波形图,虚线为t2=0.5s时的波形图,已知0<t2-t1<T,t1=0时,x=2m处的质点A正向y轴正方向振动.求:
如图实线是一列简谐横波在t1=0时的波形图,虚线为t2=0.5s时的波形图,已知0<t2-t1<T,t1=0时,x=2m处的质点A正向y轴正方向振动.求:(1)质点A的振幅、波长
(2)波的传播方向,振动周期;
(3)波速大小
(4)从t2时刻计时,x=1m处的质点的振动方程.
分析:(1)由y的最大值读出振幅A,由相邻两个波峰或波谷间的距离读出波长;
(2)t1=0时,x=2m处的质点A正向y轴正方向振动,根据波形的平移法可判断出波的传播方向;
(3)已知0<t2-t1<T,结合波的传播方向,可确定出波的传播距离△x,波速v=
;
(4)从t2时刻计时,根据波的传播方向判断出x=1m处的质点的运动方向,由v=
,求出周期,即可写出振动方程.
(2)t1=0时,x=2m处的质点A正向y轴正方向振动,根据波形的平移法可判断出波的传播方向;
(3)已知0<t2-t1<T,结合波的传播方向,可确定出波的传播距离△x,波速v=
| △x |
| △t |
(4)从t2时刻计时,根据波的传播方向判断出x=1m处的质点的运动方向,由v=
| λ |
| T |
解答:解:(1)质点A的振幅A=5cm,波长λ=4m.
(2)(3)t1=0时,x=2m处的质点A正向y轴正方向振动,根据波形的平移法得知,波的传播方向沿x轴正方向.
已知0<t2-t1<T,则该在△t=(t2-t1)时间内传播的距离为△x=2m,
则波速 v=
=
m/s=4m/s,
又由v=
得,T=
=
s=1s
(4)t2时刻,x=1m处的质点正沿y轴负方向振动,则其振动方程为
y=-Asin
t=-5sin2πt(cm)
答:(1)质点A的振幅是5cm、波长是4m.
(2)波的传播方向沿y轴正方向,振动周期是1s.
(3)波速大小是4m/s.
(4)从t2时刻计时,x=1m处的质点的振动方程是 y=-5sin2πt(cm).
(2)(3)t1=0时,x=2m处的质点A正向y轴正方向振动,根据波形的平移法得知,波的传播方向沿x轴正方向.
已知0<t2-t1<T,则该在△t=(t2-t1)时间内传播的距离为△x=2m,
则波速 v=
| △x |
| △t |
| 2 |
| 0.5 |
又由v=
| λ |
| T |
| λ |
| v |
| 4 |
| 4 |
(4)t2时刻,x=1m处的质点正沿y轴负方向振动,则其振动方程为
y=-Asin
| 2π |
| T |
答:(1)质点A的振幅是5cm、波长是4m.
(2)波的传播方向沿y轴正方向,振动周期是1s.
(3)波速大小是4m/s.
(4)从t2时刻计时,x=1m处的质点的振动方程是 y=-5sin2πt(cm).
点评:本题根据波形的平移法分析波传播的距离与波长的关系,即可求得波速.由质点的振动方向判断波的传播方向是基本功,要熟练掌握.

练习册系列答案
相关题目


 列波的波速.
列波的波速.


 m,水池里装有高度为
m,水池里装有高度为 m、折射率为
m、折射率为 的某种液体,在水池底部水平放置宽度d'=5m的平面镜,水池左壁高
的某种液体,在水池底部水平放置宽度d'=5m的平面镜,水池左壁高 m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度.
m处有一点光源S,在其正上方放有一长等于水池宽度的标尺AB,S上方有小挡板,使光源发出的光不能直接射到液面,不考虑光在水池面上的反射,求在此横截面上标尺上被照亮的长度和液面上能射出光线部分的长度.
