题目内容
一列简谐横波沿一根弹性绳传播，某一时刻质点a处于波峰，另一质点b正处于平衡位置，a、b的平衡位置相距14 m，从此时刻开始，质点b经0．14 s刚好第二次到达波峰，求这列波最大的传播速度可能是多少？
答案：
解析：
提示：
解析：
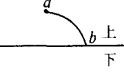
错解：假设a、b间波形如图所示．有14＝ λ，λ＝56 m，0．14＝(1＋ )T，T＝0．112 s，因ab＝ 时，波长最长，故速度最大， v＝ ＝ m／s＝500m／s，即为波最大的传播速度。
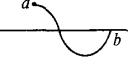
错因：波动问题往往具备多解性，如本题中，a点处于波峰，b点处于波谷，其情景还可以为图所示，此时对应波长为14＝(1＋
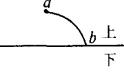
而b此时在平衡位置，可能向上运动，也可能向下运动，其对应的周期是不相同的。 正解：若ab间的波形如图时，λ=56 m，若向右传播时，0．14＝(1＋
由v＝ 答案：700 m／s 归纳：波动问题的多解性是由三个方面的因素引起的：①波传播的方向性有滑轴正向或负向两种．②波形变化的周期性．③对应可能情景的多样性．本例中，还要求从这三个方面归纳确定对应情景．
|
)λ′，λ
＝m．
)T1，T1＝0．112 s，若波向左传播时，0．14＝(1＋
)T2，T2＝0．08 s，若为图时，λ＝
m．同理有
T3＝0．08 s(向右)，T4＝0．112 s(向左)
，λ最大，T最小的，波速最大，故vmax＝
＝
m／s＝700 m／s．提示：
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目