题目内容
 如图甲所示,在真空中足够大的绝缘水平地面上,一个质量为m=0.2kg、带电荷量为q=+2.0×10-6 C的小物块处于静止状态,小物块与地面间的动摩擦因数μ=0.1.从t=0时刻开始,空间加上一个如图乙所示的场强大小和方向呈周期性变化的电场(取水平向右的方向为正方向,g取10m/s2)求:
如图甲所示,在真空中足够大的绝缘水平地面上,一个质量为m=0.2kg、带电荷量为q=+2.0×10-6 C的小物块处于静止状态,小物块与地面间的动摩擦因数μ=0.1.从t=0时刻开始,空间加上一个如图乙所示的场强大小和方向呈周期性变化的电场(取水平向右的方向为正方向,g取10m/s2)求:(1)23秒内小物块的位移大小;
(2)23秒内电场力对小物块所做的功.
分析:(1)根据牛顿第二定律求出物块在0~2s内和2~4s内的加速度,利用运动学公式求出0~2s内和2~4s内的位移,及第2s末和第4s末的速度,得到小物块做周期为4s的匀加速和匀减速运动.分别求出前22s物块的位移和第23s内的位移,再求总位移.
(2)根据动能定理求电场力对小物块所做的功.
(2)根据动能定理求电场力对小物块所做的功.
解答:解:
(1)0~2s内物块加速度a1=
=
-0.1×10=2(m/s2)
位移S1=
a1
=4m
2s末的速度为v2=a1t1=4m/s
2~4s内物块加速度a2=
=-2m/s2
位移S2=S1=4m,
4s末的速度为v4=0
则小物块做周期为4s的匀加速和匀减速运动.
第22s末小物块的速度为v=4m/s,前22s内位移为S22=
S1=44m
第23s内物块的位移为S23=vt+
a2t2,t=1s,S23=3m
故23秒内小物块的位移大小为47m.
(2)由上,物块在第23s末的速度为v23=2m/s.根据动能定理得
W-μmgS23=
m
代入解得 W=9.8J.
答:(1)23秒内小物块的位移大小为47m;
(2)23秒内电场力对小物块所做的功为9.8J.
(1)0~2s内物块加速度a1=
| qE1-μmg |
| m |
| 2×10-6×3×105 |
| 0.2 |
位移S1=
| 1 |
| 2 |
| t | 2 1 |
2s末的速度为v2=a1t1=4m/s
2~4s内物块加速度a2=
| qE2+mg |
| m |
位移S2=S1=4m,
4s末的速度为v4=0
则小物块做周期为4s的匀加速和匀减速运动.
第22s末小物块的速度为v=4m/s,前22s内位移为S22=
| 22 |
| 2 |
第23s内物块的位移为S23=vt+
| 1 |
| 2 |
故23秒内小物块的位移大小为47m.
(2)由上,物块在第23s末的速度为v23=2m/s.根据动能定理得
W-μmgS23=
| 1 |
| 2 |
| v | 2 23 |
代入解得 W=9.8J.
答:(1)23秒内小物块的位移大小为47m;
(2)23秒内电场力对小物块所做的功为9.8J.
点评:本题是物块在周期性的电场力作用下运动的问题,要抓住规律,也可以作速度-时间图象分析求解.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
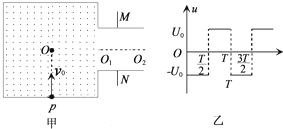 如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计)
如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计) 


