题目内容
如图所示，O1为皮带传动的主动轮的轴心，轮半径为r1，O2为从动轮的轴心，轮半径为r3； r2为固定在从动轮上的小轮半径．已知r3=2r1，r2=1.5r1．A、B和C分别是3个轮边缘上的点，质点A、B、C的向心加速度之比是（ ）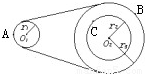
A．1：2：3
B．2：4：3
C．8：4：3
D．3：6：2
【答案】分析：对于A与B，由于皮带不打滑，线速度大小相等．对于B与C绕同一转轴转动，角速度相等，由v=ωr研究A与B的角速度关系，再根据a=ω2r求出向心加速度之比．
解答：解：对于A与B，由于皮带不打滑，线速度大小相等，即vA=vB．由v=ωr得ωA：ωB=r3：r1=2：1．
对于B与C，绕同一转轴转动，角速度相等，即ωB=ωC．
则ωA：ωB：ωC=2：1：1
根据a=ω2r可知，质点A、B、C的向心加速度之比为：8：4：3
故选C
点评：本题运用比例法解决物理问题的能力，关键抓住相等的量：对于不打滑皮带传动的两个轮子边缘上各点的线速度大小相等；同一轮上各点的角速度相同．
解答：解：对于A与B，由于皮带不打滑，线速度大小相等，即vA=vB．由v=ωr得ωA：ωB=r3：r1=2：1．
对于B与C，绕同一转轴转动，角速度相等，即ωB=ωC．
则ωA：ωB：ωC=2：1：1
根据a=ω2r可知，质点A、B、C的向心加速度之比为：8：4：3
故选C
点评：本题运用比例法解决物理问题的能力，关键抓住相等的量：对于不打滑皮带传动的两个轮子边缘上各点的线速度大小相等；同一轮上各点的角速度相同．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，O1为皮带传动的主动轮的轴心，轮半径为r1，O2为从动轮的轴心，轮半径为r3； r2为固定在从动轮上的小轮半径．已知r3=2r1，r2=1.5r1．A、B和C分别是3个轮边缘上的点，质点A、B、C的向心加速度之比是（ ）
如图所示，O1为皮带传动的主动轮的轴心，轮半径为r1，Q2为从动轮的轴心，轮半径为r2，r3为固定在从动轮上的小轮半径．已知r2=2r1，r3=1.5r1．A、B、C分别是三个轮边缘上的点，则质点A、B、C的向心加速度之比是（假设皮带不打滑）（ ）
如图所示，O1为皮带传动装置的主动轮的轴心，轮的半径为r1；O2为从动轮的轴心，轮的半径为r2；r3为从动轮固定在一起的大轮的半径．已知r2=1.5r1，r3=2r1．A、B、C分别是三轮边缘上的点，那么质点A、B、C的线速度之比是