题目内容
 如图所示,在区域I(0≤x≤L)和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,都处在xoy平面内,一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为(L.
如图所示,在区域I(0≤x≤L)和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,都处在xoy平面内,一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为(L.| L | 2 |
(1)带电粒子射入电场区域I时的初速度;
(2)电场区域Ⅱ的宽度.
分析:粒子进入电场区域做类平抛运动,根据类平抛运动规律列方程即可求解;
结合运动的合成与分解求出p点的合速度,然后根据位移公式求通过的位移,最后根据几何关系磁场宽度
结合运动的合成与分解求出p点的合速度,然后根据位移公式求通过的位移,最后根据几何关系磁场宽度
解答:解:(1)设带电粒子射入电场区域Ⅰ时的初速度为v0,
在x方向:粒子做匀速直线运动L=v0t
在y方向:粒子做初速度为零的匀加速直线运动
=
at2
且 a=
解得:v0=
(2)粒子在区域Ⅱ做匀减速直线运动,设粒子在P处的速度为vp,在x方向的分速度为
,
在y方向的分速度为vpy,电场区域Ⅱ的宽度为△x2
vpx=v0=
vpy2=2×
×
即:vpx=vpy
故:vp=
∵tanθ=
∴θ=
设粒子从P做直线运动到Q所通过的位移为S
因有:vt2-v02=2as
即:0-vp2=-2×
×S
解得:S=L△x2=Scos45°
得:△x2=
L
(1)带电粒子射入电场区域I时的初速度为
;
(2)电场区域Ⅱ的宽度为
L.
在x方向:粒子做匀速直线运动L=v0t
在y方向:粒子做初速度为零的匀加速直线运动
| L |
| 2 |
| 1 |
| 2 |
且 a=
| qE |
| m |
解得:v0=
|
(2)粒子在区域Ⅱ做匀减速直线运动,设粒子在P处的速度为vp,在x方向的分速度为
| v | px |
在y方向的分速度为vpy,电场区域Ⅱ的宽度为△x2
vpx=v0=
|
vpy2=2×
| qE |
| m |
| L |
| 2 |
即:vpx=vpy
故:vp=
|
∵tanθ=
| vpy |
| vpx |
| π |
| 4 |
设粒子从P做直线运动到Q所通过的位移为S
因有:vt2-v02=2as
即:0-vp2=-2×
| qE |
| m |
解得:S=L△x2=Scos45°
得:△x2=
| ||
| 2 |
(1)带电粒子射入电场区域I时的初速度为
|
(2)电场区域Ⅱ的宽度为
| ||
| 2 |
点评:本题考查带粒子在电场中的类平抛运动,灵活运用类平抛运动时速度偏转角的正切值求解其他量,属于常规题型.

练习册系列答案
相关题目
 和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,都处在
和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,都处在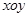 平面内,一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为
平面内,一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为 .不计粒子所受重力,求:
.不计粒子所受重力,求:

 和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,都处在
和区域Ⅱ内分别存在匀强电场,电场强度大小均为E,但方向不同.在区域I内场强方向沿y轴正方向,区域Ⅱ内场强方向未标明,都处在 平面内,一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为
平面内,一质量为m,电量为q的正粒子从坐标原点O以某一初速度沿x轴正方向射入电场区域I,从P点进入电场区域Ⅱ,到达Ⅱ区域右边界Q处时速度恰好为零.P点的坐标为 .不计粒子所受重力,求:
.不计粒子所受重力,求:
