题目内容
20. 长度为L=1.6m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
长度为L=1.6m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )| A. | 22.5N的压力 | B. | 7.5N的压力 | C. | 7.5N的拉力 | D. | 22.5N的拉力 |
分析 小球在细杆的作用下,在竖直平面内做圆周运动.对最高点受力分析,找出提供向心力的来源,结合已知量可求出最高点小球速率为2m/s时的细杆受到的力.
解答 解:小球以O点为圆心在竖直平面内作圆周运动,
当在最高点小球与细杆无弹力作用时,小球的速度为V1,则有
mg=m$\frac{{{v}_{1}}^{2}}{L}$
得:v1=$\sqrt{gL}=\sqrt{1.6×10}=4m/s$
4m/s>2m/s
则小球受到细杆的支持力
小球在O点受力分析:重力与支持力
mg-F支=m$\frac{{{v}_{2}}^{2}}{L}$
则F支=mg-m$\frac{{{v}_{2}}^{2}}{L}$=6N
所以细杆受到的压力,大小为22.5N.
故选:A
点评 小球在杆的作用下做圆周运动,在最高点杆给球的作用是由小球的速度确定.因从球不受杆作用时的速度角度突破,比较两者的速度大小,从而确定杆给球的作用力.同时应用了牛顿第二、三定律.当然还可以假设杆给球的作用力,利用牛顿第二定律列式求解,当求出力是负值时,则说明假设的力与实际的力是方向相反.

练习册系列答案
相关题目
10. 传感器是一种采集信息的重要器件,图为测定压力的电容式传感器,将电容器、灵敏电流计(零刻度在中间)的电源串联成闭合回路.当压力F作用于可动膜片电极上时,膜片产生形变,引起电容的变化,导致灵敏电流计指针偏转.在对膜片开始施加恒定的压力到膜片稳定之后,灵敏电流表指针的偏转情况为(电流从电流表正接线柱流入时指针向右偏)( )
传感器是一种采集信息的重要器件,图为测定压力的电容式传感器,将电容器、灵敏电流计(零刻度在中间)的电源串联成闭合回路.当压力F作用于可动膜片电极上时,膜片产生形变,引起电容的变化,导致灵敏电流计指针偏转.在对膜片开始施加恒定的压力到膜片稳定之后,灵敏电流表指针的偏转情况为(电流从电流表正接线柱流入时指针向右偏)( )
 传感器是一种采集信息的重要器件,图为测定压力的电容式传感器,将电容器、灵敏电流计(零刻度在中间)的电源串联成闭合回路.当压力F作用于可动膜片电极上时,膜片产生形变,引起电容的变化,导致灵敏电流计指针偏转.在对膜片开始施加恒定的压力到膜片稳定之后,灵敏电流表指针的偏转情况为(电流从电流表正接线柱流入时指针向右偏)( )
传感器是一种采集信息的重要器件,图为测定压力的电容式传感器,将电容器、灵敏电流计(零刻度在中间)的电源串联成闭合回路.当压力F作用于可动膜片电极上时,膜片产生形变,引起电容的变化,导致灵敏电流计指针偏转.在对膜片开始施加恒定的压力到膜片稳定之后,灵敏电流表指针的偏转情况为(电流从电流表正接线柱流入时指针向右偏)( )| A. | 向右偏到某一刻度后回到零刻度 | B. | 向左偏到某一刻度后回到零刻度 | ||
| C. | 向右偏到某一刻度后不动 | D. | 向左偏到某一刻度后不动 |
8. 粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
 粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )
粗糙水平面上有一个三角形木块ABC,在它的两个粗糙斜面上分别放两个质量m1和m2的木块,m1>m2,如图所示,已知三角形木块和两物体都是静止的,则粗糙水平面对三角形木块( )| A. | 有摩擦力的作用,摩擦力的方向水平向右 | |
| B. | 有摩擦力的作用,摩擦力的方向水平向左 | |
| C. | 有摩擦力的作用,但摩擦力的方向不能确定,因为m1、m2、θ1、θ2的数值并未给出 | |
| D. | 以上结论都不对 |
15.地球可近似看成球形,由于地球表面上物体都随地球自转,所以有( )
| A. | 物体在赤道处受的地球引力等于两极处,而重力小于两极处 | |
| B. | 赤道处的角速度比北纬45°大 | |
| C. | 地球上物体的向心加速度都指向地心,且赤道上物体的向心加速度比两极处大 | |
| D. | 地面上的物体随地球自转时提供向心力的是重力 |
5.以下是物理学中的四个实验装置或仪器,由图可知这四个实验装置或仪器共同的物理思想方法是( )


| A. | 假设的思想方法 | B. | 控制变量的方法 | C. | 放大的思想方法 | D. | 逻辑推理的方法 |
12. 如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )
如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )
 如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )
如图所示,一个重力为G的大砝码,用细线悬挂在O点,现在用力F拉法码,使悬线偏离竖直方向θ角时处于静止状态,此时所用拉力F的最小值为( )| A. | Gtanθ | B. | Gcosθ | C. | Gsinθ | D. | $\frac{G}{sinθ}$ |
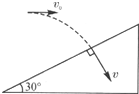 如图所示,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞击在倾角θ=30°的斜面上,求:
如图所示,以10m/s的水平初速度抛出的物体,飞行一段时间后,垂直地撞击在倾角θ=30°的斜面上,求: