题目内容
甲车以v0=10m/s,乙车以v=4m/s的速率在同一直车道中同向前进,若甲车驾驶员在乙车后方距离d处发现乙车,立即踩刹车使其车获得a=-2m/s2的加速度,为使两车不致相撞,d的值至少应为多少?
分析:为使两车不致相撞,当甲车追上乙车,两者的速度恰好相等时,两车刚好不相撞.根据速度公式和速度关系求解出时间,由位移公式和位移关系求解d的最小值.
解答:解:设经时间t,甲车速度等于乙车速度,即得 v=v0+at
得 t=
=
=3s.
在时间t内,甲乙两车位移分别为:
s甲=v0t+
at2=10×3m+
×(-2)×32m=21m
s乙=vt=4×3m=12m
故为使两车不相撞,至少相距 d=s甲-s乙=9m
答:为使两车不致相撞,d的值至少应为9m.
得 t=
| v-v0 |
| a |
| 4-10 |
| -2 |
在时间t内,甲乙两车位移分别为:
s甲=v0t+
| 1 |
| 2 |
| 1 |
| 2 |
s乙=vt=4×3m=12m
故为使两车不相撞,至少相距 d=s甲-s乙=9m
答:为使两车不致相撞,d的值至少应为9m.
点评:解决本题的关键抓住临界情况,即速度相等时恰好追上,结合位移关系进行求解.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
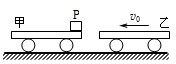
 在光滑的水平面上原来停放着一辆质量为M1=2kg的平板小车甲,它的平板是光滑的,其右端放着一个质量为m=1kg的物块P(可视为质点),另一质量为M 2=4kg的平板小车乙以v0=5m/s的速度向左运动,并跟甲车发生碰撞,如图所示,碰后甲车以6m/s的速度向左运动,物体P滑到乙车上.已知物体P跟乙车平板间的动摩擦因数为μ=0.2.求:
在光滑的水平面上原来停放着一辆质量为M1=2kg的平板小车甲,它的平板是光滑的,其右端放着一个质量为m=1kg的物块P(可视为质点),另一质量为M 2=4kg的平板小车乙以v0=5m/s的速度向左运动,并跟甲车发生碰撞,如图所示,碰后甲车以6m/s的速度向左运动,物体P滑到乙车上.已知物体P跟乙车平板间的动摩擦因数为μ=0.2.求: