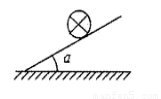题目内容
如图所示,在倾角为a的光滑斜面上放两个质量分别为m1和m2的带电小球A、B(均可视为质点),m1=2 m2,相距为L。两球同时由静止开始释放时,B球的初始加速度恰好等于零。经过一段时间后,当两球距离为L’时,A、B的加速度大小之比为a1:a2=3:2,求L’:L=?某同学求解如下:
由B球初始加速度恰好等于零,得初始时刻A对B的库仑斥力F=m2gsina,当两球距离为L’时,A球的加速度a1=,B球的加速度a2=,由a1:a2=3:2,得F’=2.5m2gsina,再由库仑力公式便可求得L’:L。
问:你同意上述解法吗?若同意,求出最终结果;若不同意,则说明理由并求出你认为正确的结果。

不同意(2分)。初始时B球受力平衡,两球相互排斥运动一段距离后,库仑力一定减小(2分),小于B球重力(1分),所以加速度a2方向应沿斜面向下,a2=(3分),得F’=0.25m2gsina(1分),所以L’:L=2:1(1分),

练习册系列答案
相关题目
 (2011?杭州一模)如图所示,在倾角为a的光滑斜面上,垂直纸面放置一根长为L,质量为m的直导体棒.当导体棒中的电流I垂直纸面向里时,欲使导体棒静止在斜面上,可加一平行于纸面的匀强磁场,当外加匀强磁场的磁感应强度B的方向由垂直斜面向上沿逆时针转至水平向左的过程中,下列关于B的大小变化的说法中,正确的是( )
(2011?杭州一模)如图所示,在倾角为a的光滑斜面上,垂直纸面放置一根长为L,质量为m的直导体棒.当导体棒中的电流I垂直纸面向里时,欲使导体棒静止在斜面上,可加一平行于纸面的匀强磁场,当外加匀强磁场的磁感应强度B的方向由垂直斜面向上沿逆时针转至水平向左的过程中,下列关于B的大小变化的说法中,正确的是( )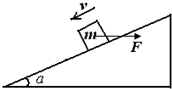 如图所示,在倾角为a的斜面上,放着一质量为m的滑块,现用水平推力F作用在滑块上,使滑块匀速下滑,斜面保持静止,求:
如图所示,在倾角为a的斜面上,放着一质量为m的滑块,现用水平推力F作用在滑块上,使滑块匀速下滑,斜面保持静止,求: (2010?南昌一模)如图所示,在倾角为a的传送带上有质量均为m的三个木块1、2,3,中间均用原长为L,劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运行,三个木块处于平衡状态.下列结论正确的是( )
(2010?南昌一模)如图所示,在倾角为a的传送带上有质量均为m的三个木块1、2,3,中间均用原长为L,劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运行,三个木块处于平衡状态.下列结论正确的是( )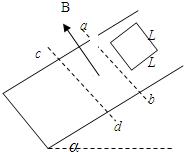 如图所示,在倾角为a的光滑斜面上,abcd区域存在着垂直斜面向上的匀强磁场,边界ab和cd都沿水平方向,ac=L,在斜面上质量为m,边长为L的正方形导线框沿斜面自由下滑,恰好匀速穿过磁场,下列说法正确的是( )
如图所示,在倾角为a的光滑斜面上,abcd区域存在着垂直斜面向上的匀强磁场,边界ab和cd都沿水平方向,ac=L,在斜面上质量为m,边长为L的正方形导线框沿斜面自由下滑,恰好匀速穿过磁场,下列说法正确的是( )