题目内容
一定质量的理想气体被活塞封闭在圆筒形的金属气缸内如图所示．活塞的质量为30kg，截面积为S=1OOcm2，活塞与气缸底之间用一轻弹簧连接，活塞可沿气缸壁无摩擦滑动但不漏气，开始使气缸水平放置，连接活塞和气缸底的弹簧处于自然长度L0=50cm．经测量，外界气温为t=27°C，大气压强为P0=1.0x1O5Pa，将气缸从水平位置缓慢地竖直立起，稳定后活塞下降了10cm；再对气缸内气体逐渐加热，若活塞上升30cm（g=10m/s2），求：①弹簧的劲度系数；
②气缸内气体达到的温度．
分析：①将气缸竖直放置稳定后，加热前，气体发生等温变化，根据玻意耳定律求得加热前缸内气体压强，由胡克定律求弹簧的劲度系数k．
②由题意知，弹簧始末两个状态都处于原长状态，说明封闭气体的体积相等．先确定初态时封闭气体的压强和温度，再由平衡条件求得末态时封闭气体的压强，由气态方程列式，可求得加热后气缸内气体达到的温度；
②由题意知，弹簧始末两个状态都处于原长状态，说明封闭气体的体积相等．先确定初态时封闭气体的压强和温度，再由平衡条件求得末态时封闭气体的压强，由气态方程列式，可求得加热后气缸内气体达到的温度；
解答：解：①将气缸竖直放置稳定后，加热前，缸内气体压强为p2，体积为V2，设k是弹簧的劲度系数．
则p2=p0+
，V2=（l0-△l）S
气缸缓慢移动时，温度不变，根据玻意耳定律得：
p1V1=p2V2
联立代入数据解得：k=500N/m．
②对气体缓慢加热后，活塞上升30cm，气体温度T3，压强为p3，体积为V3，
p3=p0+
V3=（L0+△L2-△L1）S
T1=300K
由气态方程
=
解得：T3=588K
答：①弹簧的劲度系数为500 N/m；
②气缸内气体达到的温度为588K．
则p2=p0+
| mg-k△l |
| S |
气缸缓慢移动时，温度不变，根据玻意耳定律得：
p1V1=p2V2
联立代入数据解得：k=500N/m．
②对气体缓慢加热后，活塞上升30cm，气体温度T3，压强为p3，体积为V3，
p3=p0+
| mg+k(△L2-△L1) |
| S |
V3=（L0+△L2-△L1）S
T1=300K
由气态方程
| p1V1 |
| T1 |
| p3V3 |
| T3 |
解得：T3=588K
答：①弹簧的劲度系数为500 N/m；
②气缸内气体达到的温度为588K．
点评：本题分析气体的状态参量，判断何种变化是关键，同时要能根据平衡条件求解封闭气体的压强．
练习册系列答案
相关题目
一定质量的理想气体被活塞封闭在可导热的竖直放置的气缸内，活塞横截面积为S，距气缸底部的距离为H，可沿气缸内壁无摩擦滑动．现将质量为m的沙子缓慢地一点一点地倒在活塞上，已知气体的温度与环境温度均为T0，大气压强为P0，重力加速度为g，活塞重力不计
（2008?宁夏）一定质量的理想气体被活塞封闭在可导热的气缸内，活塞相对于底部的高度为h，可沿气缸无摩擦地滑动．取一小盒沙子缓慢地倒在活塞的上表面上．沙子倒完时，活塞下降了
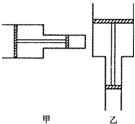如图，气缸由两个截面不同的圆筒连接而成，活塞A、B被轻质刚性细杆连接在一起，可无摩擦移动，A、B的质量分别mA=12kg，mB=8.0kg，