题目内容
质量为m=0.2千克的小球从一弹性平面处以v0=20m/s的速度竖直上抛,能上升的最大高度为h1=16m,然后落回平面,与平面发生碰撞后再次上升,上升的高度为h2=7m,而后又落回平面…直到最后静止在平面上,设小球受到的空气阻力大小恒定为Ff=0.5N,求:
(1)小球第一次上升时间和下落时间之比
(2)从小球刚开始上抛到第二次刚要落到平面时的过程中损失的机械能.
(1)小球第一次上升时间和下落时间之比
(2)从小球刚开始上抛到第二次刚要落到平面时的过程中损失的机械能.

(1)小球第一次上升过程中a1=-
=-
=-12.5m/s2
t1=
=
s=1.6s
小球第一次下落过程中a2=
=
=7.5m/s2
t2=
=
s=2.0s
=
=
(2)第一次落回地面时的速度为v1,有
2fh1=
m(
-
)
解得:v1=
m/s
第二次上升的速度为v2,有
(mg+f)h2=
m
,
解得:v2=5
m/s
小球与地面撞击时损失的能量为 △E1=
m
-
m
小球在空中损失的机械能为△E2=f(2h1+2h2)
从小球刚开始上抛到第二次落到平面之前的过程中损失的机械能为△E=△E1+△E2=
m
-
m
+f(2h1+2h2)=29.5J
答:(1)小球第一次上升时间和下落时间之比
.
(2)从小球刚开始上抛到第二次刚要落到平面时的过程中损失的机械能29.5J
| mg+f |
| m |
| 2+0.5 |
| 0.2 |
t1=
|
|
小球第一次下落过程中a2=
| mg-f |
| m |
| 2-0.5 |
| 0.2 |
t2=
|
|
| t1 |
| t2 |
| 1.6 |
| 2.0 |
| 4 |
| 5 |
(2)第一次落回地面时的速度为v1,有
2fh1=
| 1 |
| 2 |
| v | 20 |
| v | 21 |
解得:v1=
| 240 |
第二次上升的速度为v2,有
(mg+f)h2=
| 1 |
| 2 |
| v | 22 |
解得:v2=5
| 7 |
小球与地面撞击时损失的能量为 △E1=
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
小球在空中损失的机械能为△E2=f(2h1+2h2)
从小球刚开始上抛到第二次落到平面之前的过程中损失的机械能为△E=△E1+△E2=
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
答:(1)小球第一次上升时间和下落时间之比
| 4 |
| 5 |
(2)从小球刚开始上抛到第二次刚要落到平面时的过程中损失的机械能29.5J

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
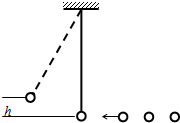 如图所示一个摆长为L=10/π2米的单摆,摆球质量为m=0.1千克,静止于平衡位置.另有质量均为m=0.1千克的小球n个与摆球在同一高度且在同一直线上,以相同的速度v=4米每秒向左运动,相邻两小球到达摆球平衡位置的时间间隔是1秒钟.每一个小球与摆球相撞后都和摆球粘在一起共同运动.(摆球和小球均视为质点,g=10m/s2)
如图所示一个摆长为L=10/π2米的单摆,摆球质量为m=0.1千克,静止于平衡位置.另有质量均为m=0.1千克的小球n个与摆球在同一高度且在同一直线上,以相同的速度v=4米每秒向左运动,相邻两小球到达摆球平衡位置的时间间隔是1秒钟.每一个小球与摆球相撞后都和摆球粘在一起共同运动.(摆球和小球均视为质点,g=10m/s2)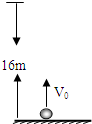 质量为m=0.2千克的小球从一弹性平面处以v0=20m/s的速度竖直上抛,能上升的最大高度为h1=16m,然后落回平面,与平面发生碰撞后再次上升,上升的高度为h2=7m,而后又落回平面…直到最后静止在平面上,设小球受到的空气阻力大小恒定为Ff=0.5N,求:
质量为m=0.2千克的小球从一弹性平面处以v0=20m/s的速度竖直上抛,能上升的最大高度为h1=16m,然后落回平面,与平面发生碰撞后再次上升,上升的高度为h2=7m,而后又落回平面…直到最后静止在平面上,设小球受到的空气阻力大小恒定为Ff=0.5N,求:
